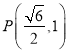题目内容
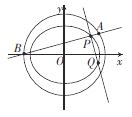
【题目】双曲线 ![]() 的右焦点为F(2,0),设A、B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,直线AB的斜率为
的右焦点为F(2,0),设A、B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,直线AB的斜率为 ![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.4
B.2
C.![]()
D.![]()
【答案】B
【解析】解:由题意可知:设A(x0 , y0),B(﹣x0 , ﹣y0),由右焦点F(2,0),则c=2 ∵以MN为直径的圆过原点O,
∴OM⊥ON,
又∵OM∥BF,ON∥AF,
∴AF⊥BF,![]() =(2﹣x0 , ﹣y0),
=(2﹣x0 , ﹣y0), ![]() =(2+x0 , y0),
=(2+x0 , y0),
∴ ![]() =(2﹣x0)(2+x0)﹣y02 ,
=(2﹣x0)(2+x0)﹣y02 ,
∴4﹣x02﹣y02=0,
即x02+y02=4,
由kAB= ![]() ,
,
∴y02= ![]() x02 ,
x02 ,
∴x02+ ![]() x02=4,
x02=4,
解得:x02= ![]() ,y02=
,y02= ![]() ,
,
代入双曲线方程得: ![]() =1,
=1,
∴7b2﹣9a2=4a2b2 , 由b2=c2﹣a2=4﹣a2 ,
∴7(4﹣a2)﹣9a2=4a2(4﹣a2),解得:a2=1或a2=7(舍),
∴a=1,
∴e=2,
故选:B.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目