题目内容
已知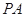 与圆
与圆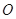 相切于点
相切于点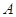 ,经过点
,经过点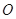 的割线
的割线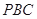 交圆
交圆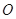 于点
于点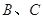 ,
,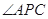 的平分线分别交
的平分线分别交 于点
于点 .
.
(1)证明: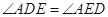 ;
;
(2)若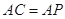 ,求
,求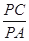 的值.
的值.
(1)证明如下 (2) 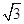
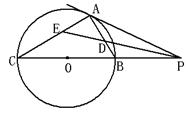
解析试题分析:(1)∵ PA是切线,AB是弦,∴∠BAP=∠C,
又∵∠APD=∠CPE,∴∠BAP+∠APD=∠C+∠CPE,∵∠ADE=∠BAP+∠APD,
∠AED=∠C+∠CPE,∴∠ADE=∠AED.
(2)由(1)知∠BAP=∠C,又∵∠APC=∠BPA, ∴△APC∽△BPA, ∴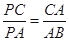 ,
,
∵ AC="AP," ∴∠APC=∠C=∠BAP,由三角形内角和定理可知,∠APC+∠C+∠CAP="180°,"
∵ BC是圆O的直径,∴∠BAC="90°," ∴∠APC+∠C+∠BAP="180°-90°=90°,"
∴∠C=∠APC=∠BAP= ×90°="30°." 在Rt△ABC中,
×90°="30°." 在Rt△ABC中, =
=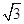 , ∴
, ∴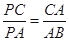 =
=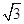 .
.
考点:几何证明
点评:关于几何证明的题目,若出现圆及切线,一般要结合到弦切角定理。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
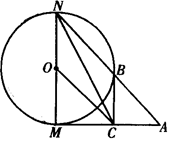
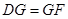 。求证:
。求证: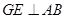
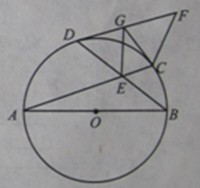
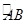 =
=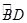 ,过C点的圆的切线与BA的延长线交于E点
,过C点的圆的切线与BA的延长线交于E点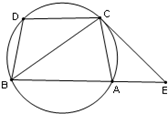
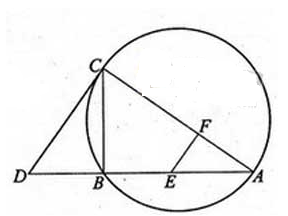
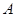 是以
是以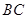 为直径的
为直径的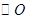 上一点,
上一点,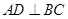 于点
于点 ,过点
,过点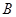 作
作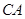 的延长线相交于点
的延长线相交于点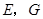 是
是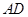 的中点,连结
的中点,连结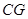 并延长与
并延长与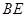 相交于点
相交于点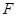 ,延长
,延长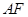 与
与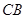 的延长线相交于点
的延长线相交于点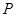 .
.
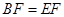 ;
;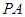 是
是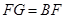 ,且
,且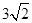 ,求
,求 和
和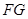 的长度.
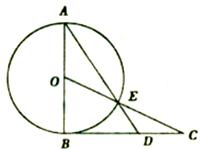
的长度.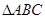 的外接圆,直线
的外接圆,直线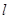 为⊙O的切线,切点为
为⊙O的切线,切点为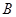 ,直线
,直线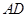 ∥
∥ 于
于 ,交⊙O于
,交⊙O于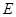 ,
,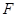 为
为 上一点,且
上一点,且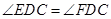 .
.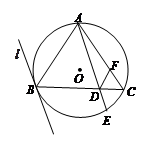
 ;
;  、
、
 是圆的两条平行弦,
是圆的两条平行弦,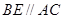 ,
,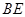 交
交 于
于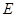 、交圆于
、交圆于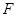 ,过
,过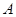 点的切线交
点的切线交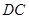 的延长线于
的延长线于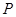 ,
, ,
,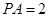 .
.
 的长;
的长;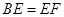 .
.