题目内容
已知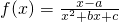 是奇函数,
是奇函数,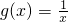 ,且对任意m•n=1,均有f(m)•g(m)+f(n)•g(n)=1等式恒成立
,且对任意m•n=1,均有f(m)•g(m)+f(n)•g(n)=1等式恒成立
(1)求函数f(x)的解析式
(2)若点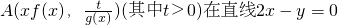 下方,求x的取值范围.
下方,求x的取值范围.
解:(1)∵f(x)为奇函数,则f(-x)=-f(x)恒成立
即
令
(2)由题意得 即
即 整理得
整理得
1°当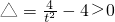 即0<t<1时,
即0<t<1时,
2°当△=0即t=1时,x∈(-∞,0)
3°当t>1时,x∈(-∞,0)
分析:(1)由f(x)为奇函数,则f(-x)=-f(x)恒成立,代入可求a,b,再由f(m)•g(m)+f(n)•g(n)=1恒成立,利用赋值,令m=n=1代入可求c
(2)由题意得 即
即 整理得
整理得 ,解不等式可得x的范围
,解不等式可得x的范围
点评:本题主要考查了奇函数的定义的应用及利用赋值求解函数的函数值,二次不等式的求解等知识的综合应用.
即

令

(2)由题意得
 即
即 整理得
整理得
1°当
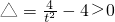 即0<t<1时,
即0<t<1时,
2°当△=0即t=1时,x∈(-∞,0)
3°当t>1时,x∈(-∞,0)
分析:(1)由f(x)为奇函数,则f(-x)=-f(x)恒成立,代入可求a,b,再由f(m)•g(m)+f(n)•g(n)=1恒成立,利用赋值,令m=n=1代入可求c
(2)由题意得
 即
即 整理得
整理得 ,解不等式可得x的范围
,解不等式可得x的范围点评:本题主要考查了奇函数的定义的应用及利用赋值求解函数的函数值,二次不等式的求解等知识的综合应用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

 是定义在
是定义在 上的函数,
上的函数, ,且
,且
 ,总有
,总有 恒成立.
恒成立. 是奇函数;
是奇函数; ,有
,有 ,
, ,求:
,求: 及
及 ;
;
 的最小值.
的最小值. 是奇函数,
是奇函数, ,且对任意m•n=1,均有f(m)•g(m)+f(n)•g(n)=1等式恒成立
,且对任意m•n=1,均有f(m)•g(m)+f(n)•g(n)=1等式恒成立 下方,求x的取值范围.
下方,求x的取值范围.