题目内容
已知平面上一定点C(2,O)和直线l:x=8,P为该平面上一动点,作PQ⊥l,垂足为Q,且 .
.(1)问点P在什么曲线上?并求出该曲线的方程;
(2)若EF为圆N:x2+(y-1)2=1的任一条直径,求
 的最大值.
的最大值.
【答案】分析:(1)根据平面向量数量积的运算性质,得4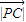 2=
2=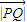 2.设P(x,y),则Q(8,y),运用距离公式化简可得3x2+4y2=48,整理得
2.设P(x,y),则Q(8,y),运用距离公式化简可得3x2+4y2=48,整理得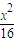 +
+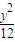 =1,由此可得点P的轨迹是以(±2,0)为焦点的椭圆;
=1,由此可得点P的轨迹是以(±2,0)为焦点的椭圆;
(2)根据题意,得|NE|=|NF|=1且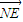 =-
=-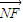 ,由此化简得
,由此化简得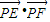 =
=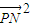 -1,根据椭圆方程与两点的距离公式,求出当P的纵坐标为-3时
-1,根据椭圆方程与两点的距离公式,求出当P的纵坐标为-3时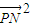 的最大值为20,由此即得
的最大值为20,由此即得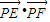 =
=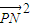 -1的最大值为19.
-1的最大值为19.
解答:解:(1)设P的坐标为P(x,y),则Q(8,y)
∵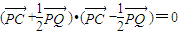 ,得:4
,得:4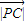 2=
2=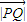 2
2
∴4[(x-2)2+y2]=[(x-8)2+(y-y)2],化简得3x2+4y2=48,
∴点P的轨迹方程为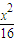 +
+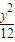 =1,此曲线是以(±2,0)为焦点的椭圆;
=1,此曲线是以(±2,0)为焦点的椭圆;
(2)∵EF为圆N的直径,∴|NE|=|NF|=1,且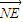 =-
=-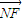
∴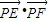 =(
=( )•(
)•(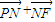 )=(
)=(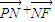 )•(
)•(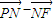 )=
)=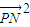 -1
-1
∵点P为椭圆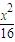 +
+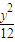 =1上的点,满足x2=16-
=1上的点,满足x2=16-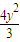
∵N(1,0),∴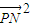 =x2+(y-1)2=-
=x2+(y-1)2=- (y+3)2+20
(y+3)2+20
∵椭圆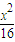 +
+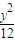 =1上点P纵坐标满足 y∈[-2
=1上点P纵坐标满足 y∈[-2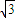 ,2
,2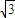 ]
]
∴当y=-3时,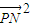 的最大值为20,故
的最大值为20,故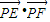 =
=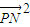 -1的最大值等于19.
-1的最大值等于19.
点评:本题给出动点P的轨迹,求其方程并研究向量数量积的最大值,着重考查了向量的数量积、椭圆的标准方程与简单性质和直线与圆等知识,属于中档题.
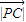 2=
2=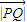 2.设P(x,y),则Q(8,y),运用距离公式化简可得3x2+4y2=48,整理得
2.设P(x,y),则Q(8,y),运用距离公式化简可得3x2+4y2=48,整理得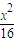 +
+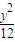 =1,由此可得点P的轨迹是以(±2,0)为焦点的椭圆;
=1,由此可得点P的轨迹是以(±2,0)为焦点的椭圆;(2)根据题意,得|NE|=|NF|=1且
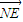 =-
=-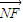 ,由此化简得
,由此化简得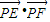 =
=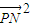 -1,根据椭圆方程与两点的距离公式,求出当P的纵坐标为-3时
-1,根据椭圆方程与两点的距离公式,求出当P的纵坐标为-3时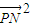 的最大值为20,由此即得
的最大值为20,由此即得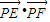 =
=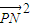 -1的最大值为19.
-1的最大值为19.解答:解:(1)设P的坐标为P(x,y),则Q(8,y)
∵
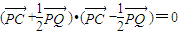 ,得:4
,得:4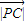 2=
2=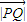 2
2∴4[(x-2)2+y2]=[(x-8)2+(y-y)2],化简得3x2+4y2=48,
∴点P的轨迹方程为
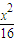 +
+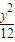 =1,此曲线是以(±2,0)为焦点的椭圆;
=1,此曲线是以(±2,0)为焦点的椭圆;(2)∵EF为圆N的直径,∴|NE|=|NF|=1,且
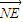 =-
=-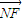
∴
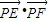 =(
=( )•(
)•(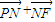 )=(
)=(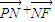 )•(
)•(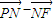 )=
)=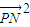 -1
-1∵点P为椭圆
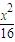 +
+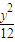 =1上的点,满足x2=16-
=1上的点,满足x2=16-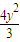
∵N(1,0),∴
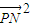 =x2+(y-1)2=-
=x2+(y-1)2=- (y+3)2+20
(y+3)2+20∵椭圆
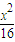 +
+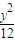 =1上点P纵坐标满足 y∈[-2
=1上点P纵坐标满足 y∈[-2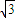 ,2
,2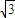 ]
]∴当y=-3时,
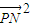 的最大值为20,故
的最大值为20,故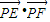 =
=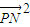 -1的最大值等于19.
-1的最大值等于19.点评:本题给出动点P的轨迹,求其方程并研究向量数量积的最大值,着重考查了向量的数量积、椭圆的标准方程与简单性质和直线与圆等知识,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目