题目内容
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,
BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点
(1)证明:直线EE1∥平面FCC1
(2)求:二面角B-FC1-C的余弦值.

【答案】
解:(1)证法一:取A1B1的中点F1,连结FF1,C1F1,
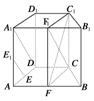
由于FF1∥BB1∥CC1,所以F1∈平面FCC1,
因此平面FCC1,即为平面C1CFF1,
连结A1D,F1C,由于A1F1綊D1C1綊CD,所以四边形A1DCF1为平行四边形,因此A1D∥F1C.
又EE1∥A1D,得EE1∥F1C,
而EE1⊄平面FCC1,F1C⊂平面FCC1,
故EE1∥平面FCC1.
证法二:因为F为AB的中点,CD=2,AB=4,AB∥CD,所以CD綊AF,
因此四边形AFCD为平行四边形,所以AD∥FC.
又CC1∥DD1,FC∩CC1=C,FC⊂平面FCC1,CC1⊂平面FCC1,
所以平面ADD1A1∥平面FCC1,
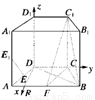
又EE1⊂平面ADD1A1,所以EE1∥平面FCC1.
(2)过D作DR⊥CD交于AB于R,

【解析】略

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明:
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明: 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点. 15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点.
15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点. (2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.
(2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.