题目内容
（2011•南通模拟）设函数f（x）=
，若f（x）为奇函数，则当0＜x≤2时，g（x）的最大值是
．
|
| 3 |
| 4 |
| 3 |
| 4 |
分析：由f（x）为奇函数，且-2≤x＜0时，f（x）=2x有最小值为f（-2）=
，根据奇函数关于原点对称可知当0＜x≤2时，f（x）=g（x）-log5（x+
）有最大值为f（2）=-
，结合函数在0＜x≤2时，g（x）=f（x）+log5（x+
）为增函数，从而可求函数g（x）的最大值
| 1 |
| 4 |
| 5+x2 |
| 1 |
| 4 |
| 5+x2 |
解答：解：由于f（x）为奇函数，
当-2≤x＜0时，f（x）=2x有最小值为f（-2）=2-2=
，
故当0＜x≤2时，f（x）=g（x）-log5（x+
）有最大值为f（2）=-
，
而当0＜x≤2时，y=log5（x+
）为增函数，
考虑到g（x）=f（x）+log5（x+
），
∵0＜x≤2时，f（x）与y=log5（x+
）在x=2时同时取到最大值，
故[g（x）]max=f（2）+log5（2+
）=-
+1=
．
答案：
当-2≤x＜0时，f（x）=2x有最小值为f（-2）=2-2=
| 1 |
| 4 |
故当0＜x≤2时，f（x）=g（x）-log5（x+
| 5+x2 |
| 1 |
| 4 |
而当0＜x≤2时，y=log5（x+
| 5+x2 |
考虑到g（x）=f（x）+log5（x+
| 5+x2 |
∵0＜x≤2时，f（x）与y=log5（x+
| 5+x2 |
故[g（x）]max=f（2）+log5（2+
| 5+22 |
| 1 |
| 4 |
| 3 |
| 4 |
答案：
| 3 |
| 4 |
点评：本题主要考查了奇函数的关于原点对称的性质的应用，利用函数的单调性求解函数的最值，属于函数知识的灵活应用．
练习册系列答案
阅读快车系列答案
相关题目
（2011•南通模拟）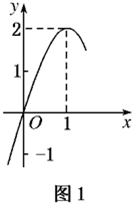
如图所示：图1是定义在R上的二次函数f（x）的部分图象，图2是函数g（x）=loga（x+b）的部分图象．