题目内容
(2011•南通模拟)若
是函数f(x)=sin2x+acos2x(a∈R,为常数)的零点,则f(x)的最小正周期是
| π | 4 |
π
π
.分析:由f(
)=sin
+acos2
=0,可求得a=-2,于是f(x)=sin2x-2cos2x转化为:f(x)=
sin(2x-
)-1,
从而可求其周期.
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
从而可求其周期.
解答:解:∵
是函数f(x)=sin2x+acos2x(a∈R,为常数)的零点,
∴f(
)=sin
+acos2
=0,
∴1+
a=0,
∴a=-2.
∴f(x)=sin2x-2cos2x
=sin2x-cos2x-1
=
sin(2x-
)-1,
∴f(x)的最小正周期为π.
故答案为:π
| π |
| 4 |
∴f(
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∴1+
| 1 |
| 2 |
∴a=-2.
∴f(x)=sin2x-2cos2x
=sin2x-cos2x-1
=
| 2 |
| π |
| 4 |
∴f(x)的最小正周期为π.
故答案为:π
点评:本题考查函数的零点,由f(
)=0求得a的值是基础,利用辅助角公式转化是关键,属于中档题.
| π |
| 4 |

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 (2011•南通模拟)
(2011•南通模拟)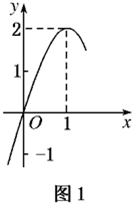 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.