题目内容
已知函数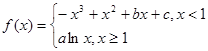
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点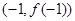 处的切线的斜率是
处的切线的斜率是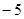 .
.
(1)求实数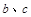 的值;
的值;
(2)求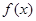 在区间
在区间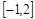 上的最大值;
上的最大值;
(3)对任意给定的正实数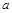 ,曲线
,曲线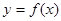 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得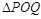 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在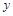 轴上?说明理由.
轴上?说明理由.
(1)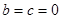 ;( Ⅱ)详见解析;( Ⅲ)详见解析.
;( Ⅱ)详见解析;( Ⅲ)详见解析.
解析试题分析:(1)当x<1时,f(x)=-x3+x2+bx+c,则f'(x)=-3x2+2x+b.依题意得: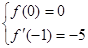 ,由此能求出实数b,c的值.(2)由
,由此能求出实数b,c的值.(2)由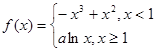 知,当-1≤x<1时,
知,当-1≤x<1时,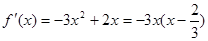 ,令f'(x)=0得
,令f'(x)=0得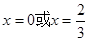 ,当x变化时,f'(x),f(x)的变化情况列表知f(x)在[-1,1)上的最大值为2.当1≤x≤2时,f(x)=alnx.当a≤0时,f(x)≤0,f(x)最大值为0;当a>0时,f(x)在[1,2]上单调递增.当aln2≤2时,f(x)在区间[-1,2]上的最大值为2;当aln2>2时,f(x)在区间[-1,2]上的最大值为aln2.(3)假设曲线y=f(x)上存在两点P、Q满足题设要求,则点P、Q只能在y轴两侧.设P(t,f(t))(t>0),则Q(-t,t3+t2),显然t≠1.由此入手能得到对任意给定的正实数a,曲线y=f(x)上存在两点P、Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上.
,当x变化时,f'(x),f(x)的变化情况列表知f(x)在[-1,1)上的最大值为2.当1≤x≤2时,f(x)=alnx.当a≤0时,f(x)≤0,f(x)最大值为0;当a>0时,f(x)在[1,2]上单调递增.当aln2≤2时,f(x)在区间[-1,2]上的最大值为2;当aln2>2时,f(x)在区间[-1,2]上的最大值为aln2.(3)假设曲线y=f(x)上存在两点P、Q满足题设要求,则点P、Q只能在y轴两侧.设P(t,f(t))(t>0),则Q(-t,t3+t2),显然t≠1.由此入手能得到对任意给定的正实数a,曲线y=f(x)上存在两点P、Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上.
解:(1)当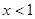 时,
时,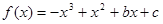 ,则
,则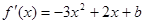 。
。
依题意得: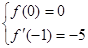 ,即
,即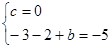 解得
解得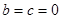
(2)由(1)知,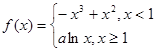
①当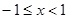 时,
时,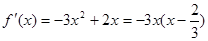 ,
,
令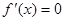 得
得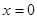 或
或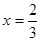
当 变化时,
变化时,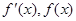 的变化情况如下表:
的变化情况如下表:
 | 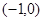 | 0 | 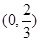 | 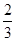 | 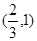 |
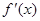 | — | 0 | + | 0 | — |
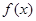 |  单调递减 单调递减 | 极小值 | 单调递增 | 极大值 | 
练习册系列答案
相关题目
|
 x2-bx(b为常数).
x2-bx(b为常数).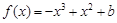 ,
,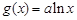 .
.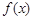 的极大值为
的极大值为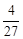 ,求实数
,求实数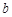 的值;
的值;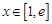 ,都有
,都有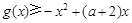 恒成立,求实数
恒成立,求实数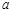 的取值范围;
的取值范围;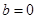 ,若
,若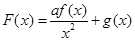 关于实数a 可线性分解,求
关于实数a 可线性分解,求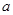 取值范围.
取值范围.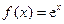 ,其中
,其中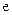 为自然对数的底数.
为自然对数的底数.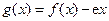 的单调区间;
的单调区间; 在点
在点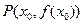 (其中
(其中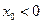 )处的切线为
)处的切线为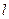 ,
,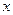 轴、
轴、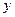 轴所围成的三角形面积为
轴所围成的三角形面积为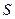 ,求
,求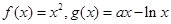 ,
, 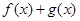 在
在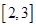 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;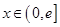 (
(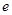 是自然常数)时,函数
是自然常数)时,函数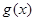 的最小值是3,若存在,求出
的最小值是3,若存在,求出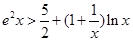 .
. +alnx(x>0).
+alnx(x>0). [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.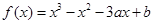 .
.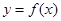 在点
在点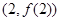 处与直线
处与直线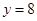 相切,求a,b的值;
相切,求a,b的值; 的单调区间.
的单调区间. ,曲线
,曲线 经过点
经过点 ,
, 处的切线为
处的切线为 .
. 、
、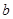 的值;
的值; ,使得
,使得 时,
时, 恒成立,求
恒成立,求