题目内容
已知三个函数y=|x|+1,y= ,y=
,y= (x+
(x+ )(x>0),其中第二个函数和第三个函数中的t为同一常数,且0<t<1,它们各自的最小值恰好是方程x3+ax2+bx+c=0的三个根.
)(x>0),其中第二个函数和第三个函数中的t为同一常数,且0<t<1,它们各自的最小值恰好是方程x3+ax2+bx+c=0的三个根.(1)求证:(a-1)2=4(b+1);
(2)设x1,x2是函数f(x)=x3+ax2+bx+c的两个极值点,求|x1-x2|的取值范围.
【答案】分析:(1)确定函数的最小值与方程x3+ax2+bx+c=0的三个根关系,证明:(a-1)2=4(b+1);
(2)利用导数与极值的关系,结合二次函数根与系数之间的关系求取值范围.
解答:解:(1)三个函数的最小值依次为1,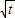 ,
,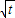 ,
,
由f(1)=0得a+b+c=-1,即c=-a-b-1,
所以f(x)=x3+ax2+bx-(a+b+1)=(x-1)[x2+(a-1)x+a+b+1],
故方程x2+(a-1)x+a+b+1=0的两个根为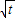 ,
,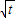 ,
,
则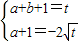 ,即4(a+b+1)=(a+1)2.
,即4(a+b+1)=(a+1)2.
(或利用判别式△=0)
(2)由题意可知x1,x2是函数f(x)=x3+ax2+bx+c的两个极值点,则x1,x2是函数f'(x)=3x2+2ax+b=0的两个根.
故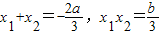 ,△=4a2-2b>0,
,△=4a2-2b>0,
所以△=4a2-3(a-1)2+12=(a+3)2,
所以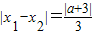 ,而
,而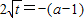 ,
,
得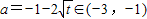 ,
,
故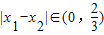 .
.
点评:本题主要考查利用函数的导数研究函数的极值问题,综合性较强.
(2)利用导数与极值的关系,结合二次函数根与系数之间的关系求取值范围.
解答:解:(1)三个函数的最小值依次为1,
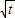 ,
,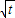 ,
,由f(1)=0得a+b+c=-1,即c=-a-b-1,
所以f(x)=x3+ax2+bx-(a+b+1)=(x-1)[x2+(a-1)x+a+b+1],
故方程x2+(a-1)x+a+b+1=0的两个根为
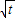 ,
,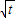 ,
,则
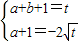 ,即4(a+b+1)=(a+1)2.
,即4(a+b+1)=(a+1)2.(或利用判别式△=0)
(2)由题意可知x1,x2是函数f(x)=x3+ax2+bx+c的两个极值点,则x1,x2是函数f'(x)=3x2+2ax+b=0的两个根.
故
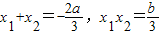 ,△=4a2-2b>0,
,△=4a2-2b>0,所以△=4a2-3(a-1)2+12=(a+3)2,
所以
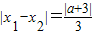 ,而
,而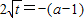 ,
,得
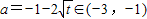 ,
,故
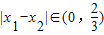 .
.点评:本题主要考查利用函数的导数研究函数的极值问题,综合性较强.

练习册系列答案
相关题目
 ,②y=sinx+
,②y=sinx+ (0<x<π),③y=log3x+logx81(x>1),其中函数的最小值为4的函数是( )
(0<x<π),③y=log3x+logx81(x>1),其中函数的最小值为4的函数是( )