题目内容
若在(x+3y2)n的展开式中,各项系数的和与各项二项式系数的和之比为512,那么(| x |
| 2 |
| x |
分析:本题对于二项式系数的和可以通过赋值令x=1来求解,而各项二项式系数之和由二项式系数公式可知为2n,最后通过比值关系为64即可求出n的值.利用二项展开式的通项公式求出通项,令x的指数为0,求出r,将r的值代入通项求出展开式的常数项.
解答:解:令 (x+3y2)n中x为1得各项系数和为4n
又展开式的各项二项式系数和为2n
∵各项系数的和与各项二项式系数的和之比为512
∴
=512
解得n=9
(
+
)n展开式的通项为 Tr+1=2rC9rx
-
r
令9-3r=0得r=3
所以展开式的常数项为 T4=23C93=672.
故答案为:672.
又展开式的各项二项式系数和为2n
∵各项系数的和与各项二项式系数的和之比为512
∴
| 4n |
| 2n |
解得n=9
(
| x |
| 2 |
| x |
| 9 |
| 2 |
| 3 |
| 2 |
令9-3r=0得r=3
所以展开式的常数项为 T4=23C93=672.
故答案为:672.
点评:本题考查求展开式的各项系数和的重要方法是赋值法、考查利用二项展开式的通项公式解决二项展开式的特定项问题,解答关键是利用展开式的各项的二项式系数的和为2n

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
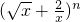 展开式中的常数项等于________.
展开式中的常数项等于________.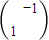 对应变换的作用下得到的点为B(-b,a).
对应变换的作用下得到的点为B(-b,a).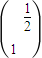 所对应变换的作用下得到的新的曲线C′的方程.
所对应变换的作用下得到的新的曲线C′的方程.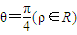 ,它与曲线
,它与曲线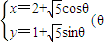 为参数)相交于两点A和B,求|AB|;
为参数)相交于两点A和B,求|AB|;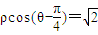 ,曲线C2的参数方程为:
,曲线C2的参数方程为: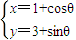 (θ为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程.
(θ为参数),试求曲线C2关于直线C1对称的曲线的直角坐标方程.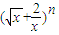 展开式中的常数项等于 .
展开式中的常数项等于 .