题目内容
已知函数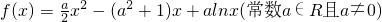
(I)讨论f(x)的单调性;
(Ⅱ)当函数f(x)在(0,+∞)上单调递增时,若x1,x2∈(0,2),且f(x1)+f(x2)=2f(a),试比较 与a的大小.
与a的大小.
解:(Ⅰ)
(1)当a<0时,f'(x)<0在(0,+∞)恒成立,f(x)在(0,+∞)递减;
(2)当a>1时,f'(x)<0解集为 ,f'(x)>0解集为
,f'(x)>0解集为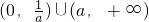 ,
,
∴f(x)在 递减,在
递减,在 上递增;
上递增;
(3)当0<a<1时,f'(x)<0解集为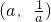 ,f'(x)>0解集为
,f'(x)>0解集为 ,
,
∴f(x)在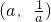 递减,在
递减,在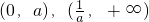 上递增;
上递增;
(4)当a=1时,f'(x)>0解集为(0,1)∪(1,+∞),
∴f(x)在(0,1)递增,在(1,+∞)上递增,且f(x)在x=1不间断,所以f(x)在(0,+∞)递增;…(4分)
(Ⅱ)由(Ⅰ)知a=1,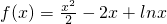 ,
,
要比较 与1的大小,只需比较x2与2-x1的大小..…(6分)
与1的大小,只需比较x2与2-x1的大小..…(6分)
因为
设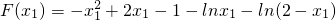 .…(8分)
.…(8分)
则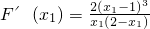
当x1∈(0,1)时,F'(x1)<0,F(x1)为减函数,
当x1∈(1,2)时,F'(x1)>0,F(x1)为增函数,
所以F(x1)≥F(1)=0…(10分)
所以f(x2)≥f(2-x1),又因为f(x)为增函数,
所以x2≥2-x1,所以 ,即
,即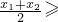 a…(12分)
a…(12分)
分析:(I)求导数可得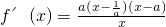 ,分a<0,a>1,0<a<1,和a=1进行讨论,可得f(x)的单调性;
,分a<0,a>1,0<a<1,和a=1进行讨论,可得f(x)的单调性;
(Ⅱ)问题转化为只需比较x2与2-x1的大小,作差后构造函数,由单调性可得最值,进而可得答案.
点评:本题考查利用导数研究函数的单调性,涉及单调性的性质和转化的思想,属中档题.

(1)当a<0时,f'(x)<0在(0,+∞)恒成立,f(x)在(0,+∞)递减;
(2)当a>1时,f'(x)<0解集为
 ,f'(x)>0解集为
,f'(x)>0解集为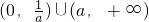 ,
,∴f(x)在
 递减,在
递减,在 上递增;
上递增;(3)当0<a<1时,f'(x)<0解集为
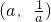 ,f'(x)>0解集为
,f'(x)>0解集为 ,
,∴f(x)在
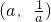 递减,在
递减,在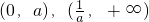 上递增;
上递增;(4)当a=1时,f'(x)>0解集为(0,1)∪(1,+∞),
∴f(x)在(0,1)递增,在(1,+∞)上递增,且f(x)在x=1不间断,所以f(x)在(0,+∞)递增;…(4分)
(Ⅱ)由(Ⅰ)知a=1,
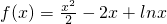 ,
,要比较
 与1的大小,只需比较x2与2-x1的大小..…(6分)
与1的大小,只需比较x2与2-x1的大小..…(6分)因为

设
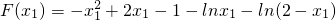 .…(8分)
.…(8分)则
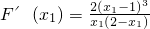
当x1∈(0,1)时,F'(x1)<0,F(x1)为减函数,
当x1∈(1,2)时,F'(x1)>0,F(x1)为增函数,
所以F(x1)≥F(1)=0…(10分)
所以f(x2)≥f(2-x1),又因为f(x)为增函数,
所以x2≥2-x1,所以
 ,即
,即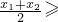 a…(12分)
a…(12分)分析:(I)求导数可得
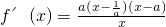 ,分a<0,a>1,0<a<1,和a=1进行讨论,可得f(x)的单调性;
,分a<0,a>1,0<a<1,和a=1进行讨论,可得f(x)的单调性;(Ⅱ)问题转化为只需比较x2与2-x1的大小,作差后构造函数,由单调性可得最值,进而可得答案.
点评:本题考查利用导数研究函数的单调性,涉及单调性的性质和转化的思想,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
,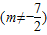
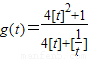 的最小值.
的最小值.
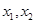 若过两点
若过两点 的直线I与x轴的交点在曲线
的直线I与x轴的交点在曲线 上,求α的值。
上,求α的值。