题目内容
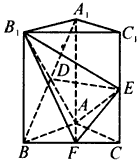
 如图,已知在直三棱柱ABC-A1B1C1中,AB=BB1=2,BC=1,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
如图,已知在直三棱柱ABC-A1B1C1中,AB=BB1=2,BC=1,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为| 5 |
| 2 |
| 5 |
| 2 |
分析:分类讨论,若把面ABA1B1 和面B1C1BC展开在同一个平面内,构造直角三角形,由勾股定理得 EF 的长度.
若把把面ABA1B1 和面A1B1C展开在同一个平面内,构造直角三角形,由勾股定理得 EF 的长度.
若把把面ACC1A1和面A1B1C1展开在同一个面内,构造直角三角形,由勾股定理得 EF 的长度.
以上求出的EF 的长度的最小值即为所求.
若把把面ABA1B1 和面A1B1C展开在同一个平面内,构造直角三角形,由勾股定理得 EF 的长度.
若把把面ACC1A1和面A1B1C1展开在同一个面内,构造直角三角形,由勾股定理得 EF 的长度.
以上求出的EF 的长度的最小值即为所求.
解答:解:直三棱柱底面为等腰直角三角形,若把面ABA1B1 和面B1C1BC展开在同一个平面内,
线段EF就在直角三角形A1EF中,由勾股定理得 EF=
=
=
..
若把把面ABA1B1 和面A1B1C展开在同一个平面内,设BB1的中点为G,则线段EF就在直角三角形EFG中,
由勾股定理得 EF=
=
=
<
.
若把把面ACC1A1和面A1B1C1展开在同一个面内,过F作与CC1行的直线,过E作与AC平行的直线,所作的两线交与点H,
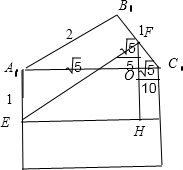
OF=
×
=
,OC1=
×
=
,
则EF就在直角三角形EFH中,由勾股定理得 EF=
=
=
>
,
综上,从E到F两点的最短路径的长度为
.
故答案为:
.
线段EF就在直角三角形A1EF中,由勾股定理得 EF=
| A1F2+A1E2 |
1+
|
| ||
| 2 |
若把把面ABA1B1 和面A1B1C展开在同一个平面内,设BB1的中点为G,则线段EF就在直角三角形EFG中,
由勾股定理得 EF=
| EG2+FG2 |
4+
|
| 5 |
| 2 |
| ||
| 2 |
若把把面ACC1A1和面A1B1C1展开在同一个面内,过F作与CC1行的直线,过E作与AC平行的直线,所作的两线交与点H,

OF=
| 1 |
| 2 |
| 2 | ||
|
| ||
| 5 |
| 1 |
| 2 |
| 1 | ||
|
| ||
| 10 |
则EF就在直角三角形EFH中,由勾股定理得 EF=
| EH2+FH2 |
(
|
3
| ||
| 2 |
| 5 |
| 2 |
综上,从E到F两点的最短路径的长度为
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查了将两个平面展在同一平面求几何体表面最小距离的问题,考查了分类讨论思想的应用.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=
如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=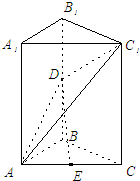 如图所示,在直三棱柱ABC-A1B1C1中,已知AB=BC=1,∠ABC=90°,
如图所示,在直三棱柱ABC-A1B1C1中,已知AB=BC=1,∠ABC=90°,