题目内容
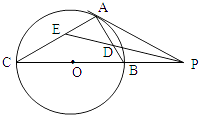
【题目】如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E.
(Ⅰ)证明:∠ADE=∠AED;
(Ⅱ)若AC=AP,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)∵PA是切线,AB是弦,
∴∠BAP=∠C.
又∵∠APD=∠CPE,
∴∠BAP+∠APD=∠C+∠CPE.
∵∠ADE=∠BAP+∠APD,∠AED=∠C+∠CPE,
∴∠ADE=∠AED.…(5分)
(Ⅱ) 由(Ⅰ)知∠BAP=∠C,
∵∠APC=∠BPA,
∵AC=AP,
∴∠APC=∠C
∴∠APC=∠C=∠BAP.
由三角形内角和定理可知,∠APC+∠C+∠CAP=180°.
∵BC是圆O的直径,
∴∠BAC=90°.
∴∠APC+∠C+∠BAP=180°﹣90°=90°.
∴ ![]() .
.
在Rt△ABC中, ![]() ,即
,即 ![]() ,
,
∴ ![]() .
.
∵在△APC与△BPA中
∠BAP=∠C,∠APB=∠CPA,
∴△APC∽△BPA.
∴ ![]() .
.
∴ ![]() .
.
【解析】(Ⅰ)根据弦切角定理,得到∠BAP=∠C,结合PE平分∠APC,可得∠BAP+∠APD=∠C+∠CPE,最后用三角形的外角可得∠ADE=∠AED;(Ⅱ)根据AC=AP得到∠APC=∠C,结合(I)中的结论可得∠APC=∠C=∠BAP,再在△APC中根据直径BC得到∠PAC=90°+∠BAP,利用三角形内角和定理可得 ![]() .利用直角三角形中正切的定义,得到
.利用直角三角形中正切的定义,得到 ![]() ,最后通过内角相等证明出△APC∽△BPA,从而
,最后通过内角相等证明出△APC∽△BPA,从而 ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目