题目内容
已知函数f(x)=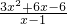 .
.
(Ⅰ)求函数f(x)在点(-1, )处的切线方程;
)处的切线方程;
(Ⅱ)求函数f(x)的极大值和极小值.
解:(Ⅰ)由已知得f′(x)=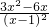 ,(3分)
,(3分)
又f′(-1)= ,
,
故所求切线方程是9x-4y+27=0.(5分)
(Ⅱ)∵f′(x)=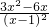 ,
,
∴f′(x)=0,
∴x1=0,x2=2.(6分)
又∵函数f(x)的定义域是x≠1的所有实数,
∴x变化时,f′(x)的变化情况如下表:
 (9分)
(9分)
∴当x=0时,函数f(x)取得极大值为6;当x=2时,函数f(x)取得极小值为18.(13分)
分析:本题可以通过计算函数的导函数求解,
(1)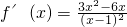 ,易得函数在所求点处的斜率,代入点斜式计算即可,
,易得函数在所求点处的斜率,代入点斜式计算即可,
(2)令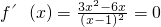 ,得两实根,比较两实根及端点的函数值.
,得两实根,比较两实根及端点的函数值.
点评:本题考查了直线的点斜式方程及利用函数的导数求解极值问题,是一道综合题,应注意掌握知识点之间的联系.
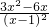 ,(3分)
,(3分)又f′(-1)=
 ,
,故所求切线方程是9x-4y+27=0.(5分)
(Ⅱ)∵f′(x)=
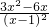 ,
,∴f′(x)=0,
∴x1=0,x2=2.(6分)
又∵函数f(x)的定义域是x≠1的所有实数,
∴x变化时,f′(x)的变化情况如下表:
 (9分)
(9分)∴当x=0时,函数f(x)取得极大值为6;当x=2时,函数f(x)取得极小值为18.(13分)
分析:本题可以通过计算函数的导函数求解,
(1)
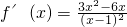 ,易得函数在所求点处的斜率,代入点斜式计算即可,
,易得函数在所求点处的斜率,代入点斜式计算即可,(2)令
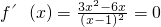 ,得两实根,比较两实根及端点的函数值.
,得两实根,比较两实根及端点的函数值.点评:本题考查了直线的点斜式方程及利用函数的导数求解极值问题,是一道综合题,应注意掌握知识点之间的联系.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|