题目内容
已知集合
，N={x||x|＜1}，则x∈M是x∈N的（ ）A．充分但不必要条件
B．必要但不充分条件
C．充分且必要条件
D．既不充分也不必要条件
【答案】分析：根据函数的定义域及绝对值值不等式的解法，我们可以求出集合M，N，然后判断出集合的关系，进而根据“谁小谁充分，谁大谁必要”的原则，即可得到结论．
解答：解：∵集合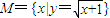
=[-1，+∞），
集合N={x||x|＜1}=（-1，1），
∵N?M
故x∈M是x∈N的必要不充分条件
故选B．
点评：本题考查的知识是充要条件，函数的定义域、绝对值不等式的解法，其中集合法判断充要条件的原则是“谁小谁充分，谁大谁必要”．
解答：解：∵集合
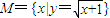=[-1，+∞），集合N={x||x|＜1}=（-1，1），
∵N?M
故x∈M是x∈N的必要不充分条件
故选B．
点评：本题考查的知识是充要条件，函数的定义域、绝对值不等式的解法，其中集合法判断充要条件的原则是“谁小谁充分，谁大谁必要”．
练习册系列答案
相关题目
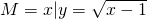，N={x|y=log2（2-x）}，则?R（M∩N）=
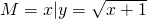，N={x||x|＜1}，则x∈M是x∈N的
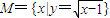，N={x|y=log2（2-x）}，则∁R（M∩N）=（ ）