题目内容
(08年上虞市质检二文) 已知平面直角坐标系中,![]() ,
,![]() 的外接圆为
的外接圆为![]() ,双曲线
,双曲线![]() 分别以
分别以![]() 为左右焦点,且离心率
为左右焦点,且离心率![]() 。
。
(Ⅰ)求圆![]() 及双曲线
及双曲线![]() 的方程;
的方程;
(Ⅱ)设双曲线![]() 的右顶点为
的右顶点为![]() ,点
,点![]() 为圆
为圆![]() 上异于
上异于![]() 的动点,过原点
的动点,过原点![]() 作直线
作直线![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() ,判断直线
,判断直线![]() 与圆
与圆![]() 的位置关系,并给出证明。
的位置关系,并给出证明。
解析:(Ⅰ)![]()
![]() 外接圆
外接圆![]() 以原点
以原点![]() 为圆心,线段
为圆心,线段![]() 为半径,故其方程为
为半径,故其方程为![]()
![]() ,又
,又![]() ,
,![]() 可得
可得![]()
![]() 所求的双曲线方程是
所求的双曲线方程是![]()
(Ⅱ)直线![]() 与圆
与圆![]() 相切。
相切。
证明:设![]() ,则
,则![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 直线
直线![]() 的方程为
的方程为![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
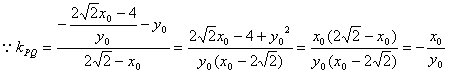
![]() 当
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]()
![]()
![]() 时,
时,![]()
故直线![]() 始终与圆
始终与圆![]() 相切。
相切。

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
