题目内容
y=Asin(ωx+φ)(|φ|<π,A>0,ω>0)的图象对称轴为x=| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 2 |
分析:根据对称轴求出函数的最大值A,相邻的两个对称中心为(π,0),(
,0)求出周期T,然后求出ω,根据一个对称中心坐标求出φ,即可求出函数的解析式.
| 5π |
| 2 |
解答:解:y=Asin(ωx+φ)(|φ|<π,A>0,ω>0)的图象对称轴为x=
交图象于点A(
,5),
所以函数的最大值为A=5,;
与点(
,5)相邻的两个对称中心为(π,0),(
,0),
所以T=3π,所以ω=
,
因为(π,0)在函数图象上,所以0=5sin(
+φ),
因为|φ|<π,所以φ=
所以所求函数的解析式为:y=5sin(
x+
)
| π |
| 4 |
| π |
| 4 |
所以函数的最大值为A=5,;
与点(
| π |
| 4 |
| 5π |
| 2 |
所以T=3π,所以ω=
| 2 |
| 3 |
因为(π,0)在函数图象上,所以0=5sin(
| 2π |
| 3 |
因为|φ|<π,所以φ=
| π |
| 3 |
所以所求函数的解析式为:y=5sin(
| 3 |
| 3 |
| π |
| 3 |
点评:本题是基础题,考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查学生对三角函数的图象的理解能力,是常考题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
若y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的最小值为-2,其图象相邻最高点与最低点横坐标之差为3π,又图象过点(0,1),则其解析式是( )
| π |
| 2 |
A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(
| ||||
D、y=2sin(
|
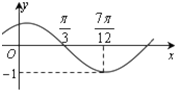 函数y=Asin(ωx+φ)(其中φ≤
函数y=Asin(ωx+φ)(其中φ≤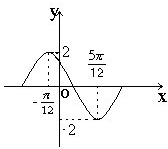 函数y=Asin (ωx+φ )在一个周期内的图象如图,此函数的解析式( )
函数y=Asin (ωx+φ )在一个周期内的图象如图,此函数的解析式( )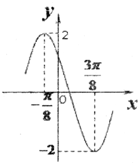 已知函数y=Asin(ωx+ψ)的图象如图所示,则函数的解析式为( )
已知函数y=Asin(ωx+ψ)的图象如图所示,则函数的解析式为( )