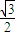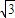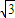题目内容
(1)过点P(-3,0)且倾斜角为30°的直线l和曲线C:
|
(2)若不等式|a-1|≥x+2y+2z,对满足x2+y2+z2=1的一切实数x,y,z恒成立,求实数a的取值范围.
分析:(1)写出直线的参数方程,代入曲线方程得到关于s 的一元二次方程,利用根与系数的关系,代入弦长公式求得 AB的长.
(2)不等式|a-1|≥x+2y+2z恒成立,只要|a-1|≥(x+2y+2z)max,利用柯西不等式9=(12+22+22)•(x2+y2+z2)≥(1•x+2•y+2•z)2求出x+2y+2z的最大值,再解关于a的绝对值不等式即可.
(2)不等式|a-1|≥x+2y+2z恒成立,只要|a-1|≥(x+2y+2z)max,利用柯西不等式9=(12+22+22)•(x2+y2+z2)≥(1•x+2•y+2•z)2求出x+2y+2z的最大值,再解关于a的绝对值不等式即可.
解答:解:(1)解:直线的参数方程为
(s 为参数),曲线
可以化为 x2-y2=4.
将直线的参数方程代入上式,得 s2-6
s+ 10 = 0.
设A、B对应的参数分别为 s1,s2,∴s1+ s2= 6
,s1•s2=10.
∴AB=|s1-s2|=
=2
.
(2)解:由柯西不等式9=(12+22+22)•(x2+y2+z2)≥(1•x+2•y+2•z)2
即x+2y+2z≤3,当且仅当
即 x=
,y=
,z=
时,x+2y+2z取得最大值3.
∵不等式|a-1|≥x+2y+2z,对满足x2+y2+z2=1的一切实数x,y,z恒成立,
只需|a-1|≥3,解得a-1≥3或a-1≤-3,∴a≥4或∴a≤-2.
即实数的取值范围是(-∞,-2]∪[4,+∞).
故答案为:a≥4或a≤-2.
|
|
将直线的参数方程代入上式,得 s2-6
| 3 |
设A、B对应的参数分别为 s1,s2,∴s1+ s2= 6
| 3 |
∴AB=|s1-s2|=
| (s1- s2)2-4s1s2 |
| 17 |
(2)解:由柯西不等式9=(12+22+22)•(x2+y2+z2)≥(1•x+2•y+2•z)2
即x+2y+2z≤3,当且仅当
|
即 x=
| 1 | ||
|
| 2 | ||
|
| 2 | ||
|
∵不等式|a-1|≥x+2y+2z,对满足x2+y2+z2=1的一切实数x,y,z恒成立,
只需|a-1|≥3,解得a-1≥3或a-1≤-3,∴a≥4或∴a≤-2.
即实数的取值范围是(-∞,-2]∪[4,+∞).
故答案为:a≥4或a≤-2.
点评:本题考查柯西不等式的应用、直线的参数方程,一元二次方程根与系数的关系,弦长公式的应用,利用 AB=|s1-s2|=
是解题的关键.
| (s1- s2)2-4s1s2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目