题目内容
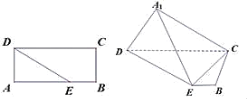
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,长轴长为4,
,长轴长为4,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,过右焦点
的左、右顶点,过右焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点.
两点.

(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)记![]() 、
、![]() 的面积分別为
的面积分別为![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(Ⅲ)设线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,记直线
,记直线![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)根据长轴长、离心率和椭圆![]() 关系可求得
关系可求得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(Ⅱ)由面积比可得到![]() ,由此利用
,由此利用![]() 表示出
表示出![]() ,根据两点在椭圆上,代入整理求得
,根据两点在椭圆上,代入整理求得![]() ,进而得到所求斜率;
,进而得到所求斜率;
(Ⅲ)利用点差法可求得![]() ,求得
,求得![]() 点坐标后可得到
点坐标后可得到![]() ;将直线方程与椭圆方程联立后可求得
;将直线方程与椭圆方程联立后可求得![]() 坐标,由三点共线可整理得到
坐标,由三点共线可整理得到![]() ,进而得到
,进而得到![]() ;将上述三个关系式代入
;将上述三个关系式代入![]() 整理可得最终结果.
整理可得最终结果.
(Ⅰ)设椭圆的焦距为![]() ,
,
![]() 椭圆长轴长为
椭圆长轴长为![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(Ⅱ)设点![]() ,
,![]() .
.
![]() ,
,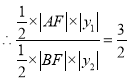 ,又
,又![]() ,
,![]() ,
, ,
,
![]() ,代入坐标可得:
,代入坐标可得: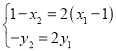 ,即
,即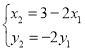 ,
,
又点![]() 、
、![]() 在椭圆
在椭圆![]() 上,
上,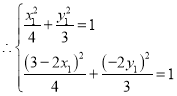 ,解得:
,解得: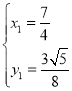 ,
,
![]() 直线
直线![]() 的斜率
的斜率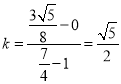 ;
;
(Ⅲ)![]() 点
点![]() ,
,![]() 在椭圆
在椭圆![]() 上,
上,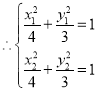 ,
,
两式相减得:![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() ,
,
令![]() 得:
得:![]() ,即
,即![]() ,
,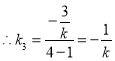 ,
,
又直线![]() 的方程为
的方程为![]() ,
,
与椭圆![]() 联立
联立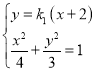 整理得:
整理得:![]() ,
,
![]() ,解得:
,解得:![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为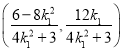 ,同理可得:点
,同理可得:点![]() 的坐标为
的坐标为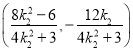 .
.
又点![]() 、
、![]() 、
、![]() 三点共线,
三点共线, ,
,
整理得:![]() ,
,
由题意知:![]() ,
,![]() ,
,![]() ,
,
由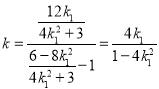 可得:
可得:![]() ,即
,即![]() .
.
![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目