题目内容
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DC=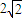 ,BC=2,则sin∠DCA= .
,BC=2,则sin∠DCA= .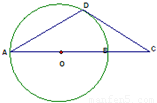
【答案】分析:连接BD、OD,由已知中AB是圆O的直径,D为圆O上一点,则∠ADB=90°,结合切割线定理,我们易求出CA的大小,从而得出圆的半径,最后利用直角三角形求出sin∠DCA的值.
解答:解:连接BD、OD,如下图所示:
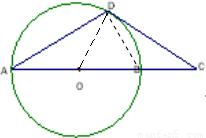
由已知中AB为圆O的直径,则∠ADB=90°
又∵CD为圆的切线,则CD2=CB•CA,即(2 )2=2CA,∴CA=4,
)2=2CA,∴CA=4,
∴AB=2,得圆的半径r=1,
在直角△CDO中,则sin∠DCA=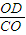 =
= .
.
故答案为: .
.
点评:本题主要考查了与圆有关的比例线段,切割线定理,以及解直角三角形等基础知识,属于基础题.
解答:解:连接BD、OD,如下图所示:

由已知中AB为圆O的直径,则∠ADB=90°
又∵CD为圆的切线,则CD2=CB•CA,即(2
 )2=2CA,∴CA=4,
)2=2CA,∴CA=4,∴AB=2,得圆的半径r=1,
在直角△CDO中,则sin∠DCA=
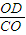 =
= .
.故答案为:
 .
.点评:本题主要考查了与圆有关的比例线段,切割线定理,以及解直角三角形等基础知识,属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
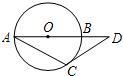 已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,求BD的长.
已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,求BD的长. 本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
 (2012•江苏)A.[选修4-1:几何证明选讲]
(2012•江苏)A.[选修4-1:几何证明选讲] 选修4-1几何证明
选修4-1几何证明