题目内容
已知函数f(x)=x2+3x|x-a|,其中a∈R.
(1)当a=2时,把函数f(x)写成分段函数的形式,并画出函数f(x)的图象;
(2)问是否存在正数a,使得函数f(x)在区间(1,3)上既有最大值又有最小值.若存在,求出a的取值范围;若不存在,请说明理由.
(1)当a=2时,把函数f(x)写成分段函数的形式,并画出函数f(x)的图象;
(2)问是否存在正数a,使得函数f(x)在区间(1,3)上既有最大值又有最小值.若存在,求出a的取值范围;若不存在,请说明理由.
分析:(1)利用绝对值的几何意义,可得分段函数,从而可得函数的图象;
(2)当a>0时,由函数的图象可知,要使得函数f(x)在开区间(m,n)内既有最大值又有最小值,则最小值一定在x=a处取得,最大值在x=
a处取得,从而可得不等式组,由此可得结论.
(2)当a>0时,由函数的图象可知,要使得函数f(x)在开区间(m,n)内既有最大值又有最小值,则最小值一定在x=a处取得,最大值在x=
| 3 |
| 4 |
解答:解:(1)当a=2时,f(x)=x2+3x|x-2|=
,此时f(x)的图象如图所示:…(5分)
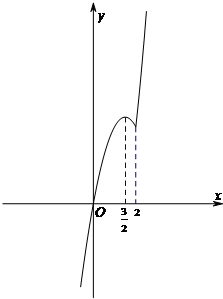
(2)当a>0时,由函数的图象可知,要使得函数f(x)在开区间(m,n)内既有最大值又有最小值,则最小值一定在x=a处取得,最大值在x=
a处取得.
由题意得
,
又f(a)=a2,f(
a)=
a2,f(1)=3a-2,f(3)=36-9a,
代入得
,
,无解.
所以满足条件的实数a不存在. …(10分)
|

(2)当a>0时,由函数的图象可知,要使得函数f(x)在开区间(m,n)内既有最大值又有最小值,则最小值一定在x=a处取得,最大值在x=
| 3 |
| 4 |
由题意得
|
又f(a)=a2,f(
| 3 |
| 4 |
| 9 |
| 8 |
代入得
|
|
所以满足条件的实数a不存在. …(10分)
点评:本题考查函数的最值,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|