题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<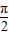 )(x∈R)的部分图象如图所示.
)(x∈R)的部分图象如图所示.(Ⅰ)求f(x)的解析式;
(Ⅱ)设
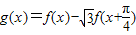 ,且
,且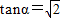 ,求g(α)的值.
,求g(α)的值.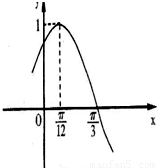
【答案】分析:(Ⅰ)通过函数的图象求出振幅和周期,求出ω,利用特殊点求解φ,即可求解f(x)的解析式;
(Ⅱ)利用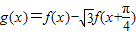 ,求出表达式,转化g(α)为tanα的形式,然后求解g(α)的值.
,求出表达式,转化g(α)为tanα的形式,然后求解g(α)的值.
解答:解:(Ⅰ)由图象可得A=1,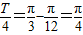 ,T=π,ω=
,T=π,ω= =2.
=2.
又图象经过( ,0),∴sin(
,0),∴sin( )=1,
)=1,
∵|φ|< ,∴φ=
,∴φ=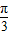 ,
,
所以f(x)的解析式f(x)=sin(2x+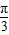 );
);
(Ⅱ)设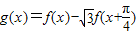 =sin(2x+
=sin(2x+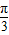 )+
)+ sin(2x-
sin(2x-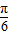 )=2sin2x,
)=2sin2x,
所以g(α)=2sin2α=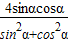 =
=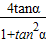 ,
,
∵ ,
,
所以g(α)=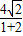 =
=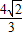 .
.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的值的求法,同角三角函数的基本关系式的应用,考查计算能力.
(Ⅱ)利用
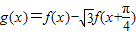 ,求出表达式,转化g(α)为tanα的形式,然后求解g(α)的值.
,求出表达式,转化g(α)为tanα的形式,然后求解g(α)的值.解答:解:(Ⅰ)由图象可得A=1,
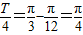 ,T=π,ω=
,T=π,ω= =2.
=2.又图象经过(
 ,0),∴sin(
,0),∴sin( )=1,
)=1,∵|φ|<
 ,∴φ=
,∴φ=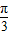 ,
,所以f(x)的解析式f(x)=sin(2x+
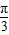 );
);(Ⅱ)设
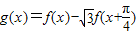 =sin(2x+
=sin(2x+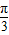 )+
)+ sin(2x-
sin(2x-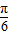 )=2sin2x,
)=2sin2x,所以g(α)=2sin2α=
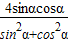 =
=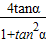 ,
,∵
 ,
,所以g(α)=
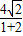 =
=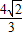 .
.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的值的求法,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目