题目内容
定义在R上的函数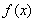
，如果存在函数
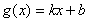(k,b为常数），使得
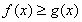对一切实数x都成立，则称
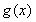为函数
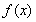的一个承托函数．现有如下命题：
①对给定的函数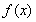
，其承托函数可能不存在，也可能有无数个．
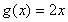②函数
为函数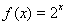
的一个承托函数．
③定义域和值域都是R的函数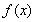
不存在承托函数．
其中正确命题的序号是：( )
A．① B．② C．①③ D．②③
【答案】
A
【解析】
试题分析：对于①，若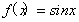
，则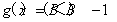
，就是它的一个承托函数，且有无数个，再如
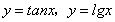就没有承托函数，∴命题①正确；
对于②，∵当
时，
，∴
，
∴
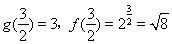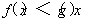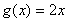不是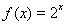
的一个承托函数，故错误；
对于③如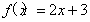
存在一个承托函数
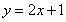，故错误；
故选A．
考点：新定义函数，一次函数、指数函数的性质.
练习册系列答案
相关题目
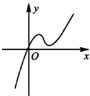定义在R上的函数f（x）满足f（4）=1．f'（x）为f（x）的导函数，已知函数y=f'（x）的图象如右图所示．若两正数a，b满足f（2a+b）＜1，则| b+2 |
| a+2 |
A、(
| ||||
B、（
| ||||
C、（
| ||||
| D、（3，+∞） |
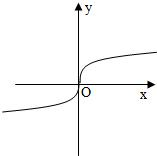
17、已知定义在R上的函数y=f（x）的图象如图所示定义在R上的函数f（x）满足f（1）=1，f′（x）是f（x）的导数．函数y=f′（x）的图象如图所示．若两个正数x，y满足f（x+y）＜1，则
的取值范围是（ ）
| y |
| x+1 |
| A、（0，1） |
| B、[0，1） |
| C、[0，+∞） |
| D、（1，+∞） |
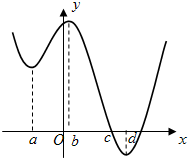已知定义在R上的函数f（x），其导函数f′（x）的大致图象如图所示，则下列叙述正确的是（ ）