题目内容
设A,B为直线
与圆
的两个交点，则|AB|=（ ）
| A．1 | B． | C． | D．2 |
D
解析试题分析：直线与圆的交点弦长可由两种方法得到:①求出圆心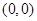
到直线的距离
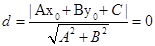,所以直径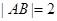
②直线与圆联立方程,由弦长公式
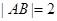来求得.故选D.
考点：直线与圆的交点弦长
练习册系列答案
相关题目
已知圆
，圆
与圆
关于直线
对称，则圆的方程为（ ）
A． | B． |
C． | D． |
若坐标原点在圆
的内部，则实数m的取值范围是（ ）
A． | B． |
C． | D． |
若点
和点
到直线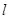
的距离依次为
和
，则这样的直线有（ ）
| A．条 | B．条 | C． 条 | D． 条 |
直线
与圆
有两个不同交点,则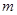
满足（ ）．
A． | B． | C． | D． |
在平面直角坐标系内，若圆
：
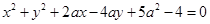的圆心在第二象限内，则实数
的取值范围为( )
A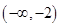． | B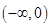． | C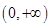． | D． |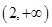
已知直线
与曲线
有交点，则( )
A． | B． | C． | D． |
已知直线
与直线
平行且与圆
相切，则直线的方程为（ ）
A． | B． 或 |
C． | D．或 |
已知在平面直角坐标系
中，圆
的方程为
，直线
过点
且与直线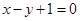
垂直.若直线与圆交于
两点，则
的面积为（ ）
| A．1 | B． | C．2 | D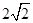． |