Question

若定义域为R的奇函数f（x）满足f（1+x）=-f（x），则下列结论：
①f（x）的图象关于点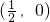对称；②f（x）的图象关于直线对称；③f（x）是周期函数，且2个它的一个周期；④f（x）在区间（-1，1）上是单调函数，其中正确结论的序号是________．（填上你认为所有正确结论的序号）

Answer 1

②③
分析：根据f（2+x）=-f（x+1）=f（x）可断定函数f（x）为周期函数，故可知③正确；根据f（x）为奇函数，可知函数关于原点对称
根据周期性及f（1+x）=-f（x）可知函数关于（k，0）对称，排除①；根据f（1+x）=-f（x）可推知f（x+）=f（-x）进而推知f（x）的图象关于直线对称；f（x）在区间（-1，0）上和在（0，1）上均为单调函数，但在（-1，1）不是单调函数，故④不正确．
解答：f（2+x）=-f（x+1）=f（x），
∴函数是以2为周期的周期函数，故③是正确的．
∵f（x）为定义域为R的奇函数，
∴f（x）函数图象关于原点对称，
∵f（x）为周期函数，周期为2且f（1+x）=-f（x），
∴f（x）函数图象关于点（k，0）（k∈Z）对称，故①不对．
∵f（1+x）=-f（x）
∴f（x+）=f（x-+1）=-f（x-）=f（-x）
∴f（x）的图象关于直线对称，故②正确．
f（x）在区间（-1，0）上和在（0，1）上均为单调函数，但在（-1，1）不是单调函数，故④不正确．
点评：本题主要考查函数单调性和奇偶性的综合应用．属基础题．