题目内容
已知定义域为R的奇函数y=f(x),当x>0时,f(x)=3x-2
(Ⅰ)若f(a)=
,求a的值;
(Ⅱ)解不等式f(x)<1.
(Ⅰ)若f(a)=
| 2 | 3 |
(Ⅱ)解不等式f(x)<1.
分析:(Ⅰ)利用函数是奇函数,先求出f(x)的表达式,然后由f(a)=
,可求a的值;
(Ⅱ)利用不等式的性质解不等式即可.
| 2 |
| 3 |
(Ⅱ)利用不等式的性质解不等式即可.
解答:解:(Ⅰ)∵f(x)为R上的奇函数,
∴f(0)=0,
若x<0,则-x>0,
∴f(-x)=3-x-2,则-f(x)=3-x-2
得f(x)=-3-x+2,(x<0).
∴f(x)=
.
①由
,得a=log38-1.
②由
,得a=1-log34.
故a=log38-1或a=1-log34.
(Ⅱ)方法一:∵f(x)=
∴(1)
⇒0<x<1,
(2)
⇒x=0,
(3)
⇒x<0.
故不等式f(x)<1的解集为(-∞,1)…(12分)
方法二:(图象法)如图,画出y=f(x)的图象,由图可得
不等式f(x)<1的解集为(-∞,1)
方法3:(单调性法)
(1)当x>0时,f(x)=3x-2为增函数,
∵f(1)=1,
∴f(x)<1?f(x)<f(1)?0<x<1.
(2)当x=0时,f(x)=0<1成立
(3)当x<0时,∵f(x)为R上的奇函数,
∴f(x)为(-∞,0)上的增函数,
由图象可得x→0时,f(x)→1,
则x<0时,f(x)<1恒成立.
∴f(0)=0,
若x<0,则-x>0,
∴f(-x)=3-x-2,则-f(x)=3-x-2
得f(x)=-3-x+2,(x<0).
∴f(x)=
|
①由
|
②由
|
故a=log38-1或a=1-log34.
(Ⅱ)方法一:∵f(x)=
|
∴(1)
|
(2)
|
(3)
|
故不等式f(x)<1的解集为(-∞,1)…(12分)
方法二:(图象法)如图,画出y=f(x)的图象,由图可得

不等式f(x)<1的解集为(-∞,1)
方法3:(单调性法)
(1)当x>0时,f(x)=3x-2为增函数,
∵f(1)=1,
∴f(x)<1?f(x)<f(1)?0<x<1.
(2)当x=0时,f(x)=0<1成立
(3)当x<0时,∵f(x)为R上的奇函数,
∴f(x)为(-∞,0)上的增函数,
由图象可得x→0时,f(x)→1,
则x<0时,f(x)<1恒成立.
点评:本题主要考查函数奇偶性的应用,以及不等式的解法,要注意利用分段函数,进行分类讨论此题有个错误解法,请看:
解:单调性的错误解法:当x>0时,f(x)=3x-2为增函数,∵f(x)为R上的奇函数,∴f(x)为R上的增函数,∵f(1)=1,∴f(x)<1?f(x)<f(1)?x<1
错因:∵f(x)在R上不是增函数,而是在(-∞,0)与(0,+∞)上均为增函数就象y=
在(-∞,0)与(0,+∞)上均为减函数,而不能说在其定义域上是减函数一样.
解:单调性的错误解法:当x>0时,f(x)=3x-2为增函数,∵f(x)为R上的奇函数,∴f(x)为R上的增函数,∵f(1)=1,∴f(x)<1?f(x)<f(1)?x<1
错因:∵f(x)在R上不是增函数,而是在(-∞,0)与(0,+∞)上均为增函数就象y=
| 1 |
| x |

练习册系列答案
相关题目
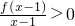 的解集为________(结果用区间表示).
的解集为________(结果用区间表示).