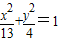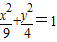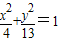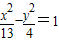题目内容
已知椭圆的两个焦点是（-3，0），（3，0），且点（0，2）在椭圆上，则椭圆的标准方程是（ ）
分析：根据椭圆方程为标准方程，及椭圆的两个焦点是（-3，0），（3，0），且点（0，2）在椭圆上，可得相应几何量，从而得解．
解答：解：由题意，因为椭圆的两个焦点是（-3，0），（3，0），
所以c=3，
又因为椭圆过点（0，2），
所以b=2，
根据a2=b2+c2，可得a=
．
故椭圆的标准方程为：
+
=1
故选A．
所以c=3，
又因为椭圆过点（0，2），
所以b=2，
根据a2=b2+c2，可得a=
| 13 |
故椭圆的标准方程为：
| x2 |
| 13 |
| y2 |
| 4 |
故选A．
点评：本题以椭圆的性质为载体，考查椭圆的标准方程，解题的关键是正确运用椭圆的几何性质．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
已知椭圆的两个焦点是（-4，0），（4，0），且过点（0，3），则椭圆的标准方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
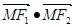=0的点M总在椭圆的内部，则椭圆的离心率的取值范围是 ▲
的两个焦点是F1，F2，点P在椭圆上，且PF1⊥F1F2，那么|PF2|= ．
