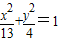题目内容
已知椭圆
的两个焦点是F1，F2，点P在椭圆上，且PF1⊥F1F2，那么|PF2|= ．
【答案】分析：先求出焦点坐标，进而根据条件求出P点坐标和|PF1|然后利用椭圆的定义PF1|+|PF2|=2a=2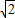
求出答案．
解答：解：∵椭圆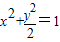
∴F1=（0，1），F2=（0，-1）
∵PF1⊥F1F2
∴P（±
，1）
∴|PF1|=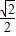
，|
由椭圆的定义可知|PF1|+|PF2|=2a=2
，
∴|PF2|=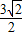
故答案为：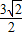
点评：本题主要考查了椭圆的应用，椭圆的简单性质和椭圆的定义．考查了考生对所学知识的综合运用．
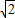求出答案．解答：解：∵椭圆
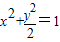
∴F1=（0，1），F2=（0，-1）
∵PF1⊥F1F2
∴P（±
，1）∴|PF1|=
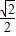，|由椭圆的定义可知|PF1|+|PF2|=2a=2
，∴|PF2|=
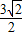
故答案为：
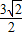
点评：本题主要考查了椭圆的应用，椭圆的简单性质和椭圆的定义．考查了考生对所学知识的综合运用．
练习册系列答案
相关题目
已知椭圆的两个焦点是（-4，0），（4，0），且过点（0，3），则椭圆的标准方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
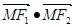=0的点M总在椭圆的内部，则椭圆的离心率的取值范围是 ▲
