Question

（08年东城区统一练习一文）（13分）

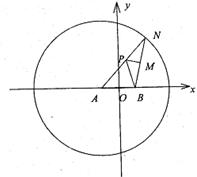
如图，在平面直角坐标系中，N为圆A：上的一动点，点B（1，0），点M是BN中点，点P在线段AN上，且

   （I）求动点P的轨迹方程；

   （II）试判断以PB为直径的圆与圆=4的位置关系，并说明理由.

Answer 1

 解析：（I）解：由点M是BN中点，又，

       可知PM垂直平分BN.所以|PN|=|PB|，又|PA|+|PN|=|AN|，

       所以|PA|+|PB|=4.

       由椭圆定义知，点P的轨迹是以A，B为焦点的椭圆.

       设椭圆方程为，

       由2a=4，2c=2，可得a²=4，b²=3.

       可知动点P的轨迹方程为…………………………6分

   （II）解：设点的中点为Q，则，

       ，

       即以PB为直径的圆的圆心为，半径为，

       又圆的圆心为O（0，0），半径r₂=2，

       又

       =，

       故|OQ|=r₂－r₁，即两圆内切.……………………………………………………13分