题目内容
在正三棱锥S—ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若侧棱SA=2
,则正三棱锥S—ABC外接球的表面积是( )A.12π B.32π C.36π D.48π
答案:C
解析:∵MN⊥AM,∴SB⊥AM.又∵SB⊥AC,
∴SB⊥平面SAC.∴SA、SB、SC两两垂直.
将S—ABC补成正方体,则S—ABC的外接球与正方体的外接球相同,则球的直径等于正方体的对角线长,∴2R=.∴R=3,S=36π.
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
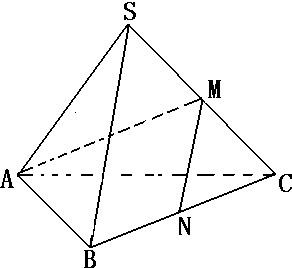如图，在正三棱锥S-ABC中，M、N分别为棱SC、BC的中点，并且AM⊥MN，若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中，D是AB的中点，且SD与BC成45°角，则SD与底面ABC所成角的正弦为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|