题目内容
(本题满分16分)A、B是函数f(x)=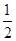 +
+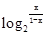 的图象上的任意两点,且
的图象上的任意两点,且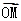 =
=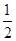 (
(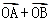 ),已知点M的横坐标为
),已知点M的横坐标为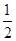 .
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f(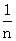 )+f(
)+f(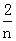 )+…+f(
)+…+f(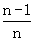 ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为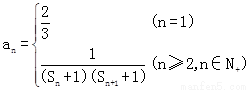 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<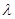 (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数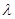 的取值范围.
的取值范围.
【答案】
(Ⅰ)证明:设A(x1,y1),B(x2,y2),M(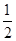 ,ym),由
,ym),由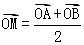 得
得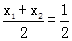
即x1+x2=1.
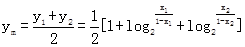
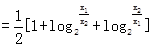
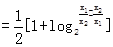
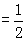
即M点的纵坐标为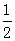 . …………………………………………………4分
. …………………………………………………4分
(Ⅱ)当n≥2时,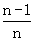 ∈(0,1),又
∈(0,1),又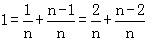 =…=x1+x2,
=…=x1+x2,
∴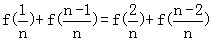 =…=f(x1)+f(x2)=y1+y2=1.
=…=f(x1)+f(x2)=y1+y2=1.
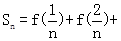 …
…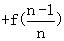 ,又
,又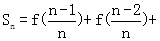 …
…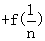 ,
,
∴2Sn=n-1,则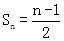 (n≥2,n∈N+). ……………………………10分
(n≥2,n∈N+). ……………………………10分
(Ⅲ)由已知T1=a1=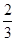 ,n≥2时,
,n≥2时,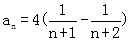 ,
,
∴Tn=a1+a2+…+an=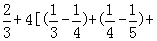 …
…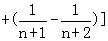 =
=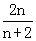 .
.
当n∈N+时,Tn<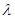 (Sn+1+1),即
(Sn+1+1),即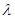 >
>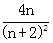 ,n∈N+恒成立,则
,n∈N+恒成立,则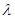 >
>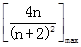 .
.
而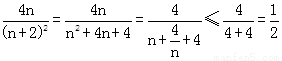 (n=2时“=”成立),
(n=2时“=”成立),
∴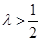 ,∴实数
,∴实数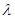 的取值范围为(
的取值范围为(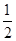 ,+∞). ……………………16分
,+∞). ……………………16分
【解析】略

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 +
+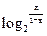 的图象上的任意两点,且
的图象上的任意两点,且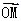 =
=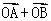 ),已知点M的横坐标为
),已知点M的横坐标为 )+f(
)+f( )+…+f(
)+…+f(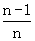 ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;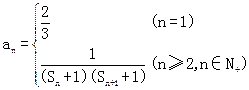 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<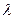 (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数 是奇函数,定义域为区间D(使表达式有意义的实数x
的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x
的集合). ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明; (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值. -t
-t )·
)·