Question

(本小题满分12分)

如图，四棱锥P－ABCD中，PA⊥底面ABCD，底面ABCD为直角梯形，AB∥CD，BA⊥AD，且CD=2AB．

（1）若AB=AD=,直线PB与CD所成角为，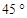

①求四棱锥P－ABCD的体积；

②求二面角P－CD－B的大小；

（2）若E为线段PC上一点，试确定E点的位置，使得平面EBD垂直于平面ABCD，并说明理由．

 

Answer 1

【答案】

（1）(1)V_P－ABCD=·PA·S_ABCD=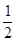a³．(2)二面角P－CD－B为45⁰．

(2) 当点E在线段PC上，且满足PE ：EC=2 ：1时，平面EBD垂直于平面ABCD．见解析。

【解析】

试题分析：

(1)∵AB∥CD，∴∠PBA是PB与CD所成角，

从而可以得到V_P－ABCD=·PA·S_ABCD=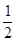a³，又因为 ∵AB⊥AD，CD∥AB∴CD⊥AD

又PA⊥底面ABCD∴∠PDA是二面角P－CD－B的平面角，进而解得。

 (2) 当点E在线段PC上，且满足PE ：EC=2 ：1时，平面EBD垂直于平面ABCD．

结合猜想，运用面面垂直判定定理得到。

（1）∵AB∥CD，∴∠PBA是PB与CD所成角，

即∠PBA=45⁰ ， ∴在直角△PAB中，PA=AB=a 

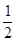(1)V_P－ABCD=·PA·S_ABCD=a³．

(2)∵AB⊥AD，CD∥AB

 ∴CD⊥AD

又PA⊥底面ABCD

∴PA⊥CD

∴CD⊥平面PAD

∴CD⊥PD

∴∠PDA是二面角P－CD－B的平面角

在直角△PDA中,∵PA=AD=a

∴∠PDA=45⁰

即二面角P－CD－B为45⁰．

(2) 当点E在线段PC上，且满足PE ：EC=2 ：1时，平面EBD垂直于平面ABCD．

理由如下：连AC、BD交于O点，连EO.

由△AOB∽△COD，且CD=2AB

∴CO=2AO

∴PE:EC=AO:CO =1:2

∴PA∥EO 

∵PA⊥底面ABCD，

∴EO⊥底面ABCD.

又EO在平面EBD内，

∴平面EBD垂直于平面ABCD  

考点：本题主要考查了空间中体积和二面角的求解，以及面面垂直的证明的综合运用。

点评：解决该试题的关键熟练掌握几何体的结构特征，进而得到空间中点、线、面的位置关系，结合有关定理进行证明即可，并且也有利于建立空间之间坐标系，利用向量的有关知识解决空间角与空间距离等问题．