题目内容
在正方体ABCD－A1B1C1D1中，E、F分
别为棱AA1、CC1的中点，则在空间中与三条直线A1D1、EF、CD都相交的直线有 条.
在A1D1上任取一点P，过点P与直线EF作一个平面α，因CD与平面α不平行，所以它们相交，设α∩CD＝Q，连结PQ，则PQ与EF必然相交，即PQ为所求直线.由点P的任意性，知有无数条直线与A1D1、EF、CD都相交.
答案：无数
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
在正方体ABCD-A1B1C1D1中，E是棱A1B1的中点，则A1B与D1E所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在正方体ABCD-A1B1C1D1中，AB与平面A1BC1所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（本小题满分12分）
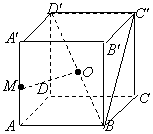
在正方体ABCD－A′B′C′D′中，点M是棱AA′的中点，点O是对角线BD′的中点.
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅱ）求二面角M－BC′－B′的大小；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；