题目内容
已知函数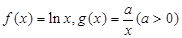 ,设
,设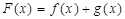
(1)求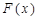 的单调区间;
的单调区间;
(2)若以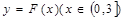 图象上任意一点
图象上任意一点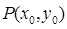 为切点的切线的斜率
为切点的切线的斜率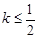 恒成立,求实数的最小值;
恒成立,求实数的最小值;
(3)是否存在实数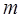 ,使得函数
,使得函数 的图象与
的图象与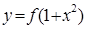 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出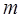 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
【答案】
(1)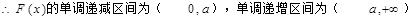 ;
;
(2)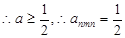 ;(3)
;(3)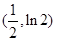 .
.
【解析】本试题主要是考查了导数在研究函数中的运用,判定函数的单调性和求解切线方程,以及解决方程根的问题的转换与划归思想的运用。
(1)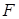
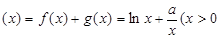 )
)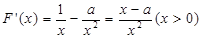
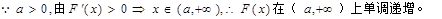
由 。
。
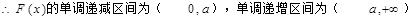
(2)
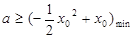 当
当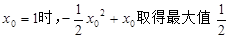
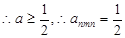
(3)若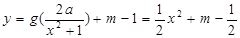 的图象与
的图象与
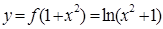 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即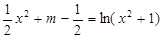 有四个不同的根,亦即
有四个不同的根,亦即
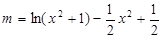 有四个不同的根。
有四个不同的根。
令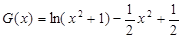 ,
,
则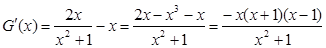 。
。
当变化时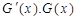 的变化情况如下表:
的变化情况如下表:
|
|
|
(-1,0) |
(0,1) |
(1, |
|
|
+ |
- |
+ |
- |
|
|
↗ |
↘ |
↗ |
↘ |
由表格知: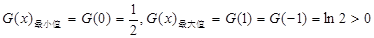 。
。
画出草图和验证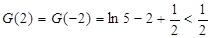 可知,当
可知,当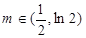 时,
时,


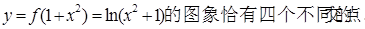

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
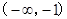
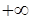 )
)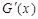 的符号
的符号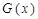 的单调性
的单调性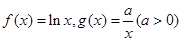 ,设
,设
 的单调区间;
的单调区间;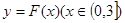 图象上任意一点
图象上任意一点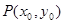 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数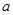 的最小值;
的最小值;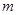 ,使得函数
,使得函数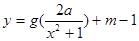 的图象与
的图象与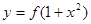 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出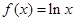 ,
,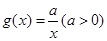 ,设
,设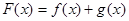 .
. 的单调区间;
的单调区间;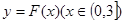 图象上任意一点
图象上任意一点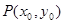 为切点的切线的斜率
为切点的切线的斜率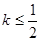
 的最小值.
的最小值.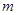 ,使得函数
,使得函数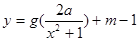 的图象与
的图象与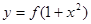 的图
的图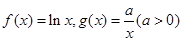 ,设
,设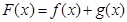
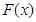 的单调区间;
的单调区间; )图像上任意一点
)图像上任意一点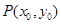 为切点的切线的斜率
为切点的切线的斜率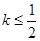 恒成立,求实数
恒成立,求实数 的最小值;
的最小值; 都有
都有 成立,求实数
成立,求实数