题目内容
（本题满分12分）
甲、乙、丙三人进行象棋比赛，每两人比赛一场，共赛三场．每场比赛胜者得3
分，负者得0分，没有平局，在每一场比赛中，甲胜乙的概率为
，甲胜丙的概率为
，乙胜丙的概率为
(1)求甲获第一名且丙获第二名的概率：
(2)设在该次比赛中，甲得分为ξ，求ξ的分布列和数学期望。
甲、乙、丙三人进行象棋比赛，每两人比赛一场，共赛三场．每场比赛胜者得3
分，负者得0分，没有平局，在每一场比赛中，甲胜乙的概率为
，甲胜丙的概率为，乙胜丙的概率为(1)求甲获第一名且丙获第二名的概率：
(2)设在该次比赛中，甲得分为ξ，求ξ的分布列和数学期望。
解：(1)甲获第一，则甲胜乙且甲胜丙，
∴甲获第一的概率为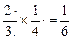
……………2分
丙获第二，则丙胜乙，其概率为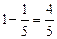
…………4分
∴甲获第一名且丙获第二名的概率为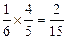
……………6分
(2)ξ可能取的值为O、3、6…………………………7分
甲两场比赛皆输的概率为
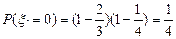……8分
甲两场只胜一场的概率为
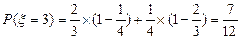………9分
甲两场皆胜的概率为
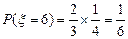……………lO分
∴ξ的分布列为
ξ 0 3 6
P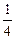
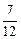
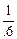
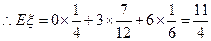…………l2分
∴甲获第一的概率为
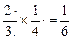……………2分丙获第二，则丙胜乙，其概率为
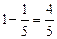…………4分∴甲获第一名且丙获第二名的概率为
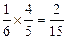……………6分(2)ξ可能取的值为O、3、6…………………………7分
甲两场比赛皆输的概率为
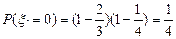……8分甲两场只胜一场的概率为
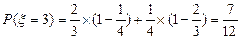………9分甲两场皆胜的概率为
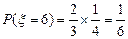……………lO分∴ξ的分布列为
ξ 0 3 6
P
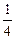
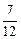
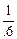
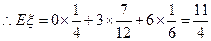…………l2分略
练习册系列答案
相关题目
等于3中三等奖．
（Ⅱ）求中奖的概率．
,若一周5个工作日内无故障,则可获得利润10万元;仅有一个工作日发生故障可获得利润5万元; 仅有两个工作日发生故障不获利也不亏损;有三个或三个以上工作日发生故障就要亏损2万元.求:
010年广洲亚运会，某班拟选派4人为志愿者参与亚运会，经过初选确定5男4女共9名同学成为候选人，每位候选人当选志愿者的机会均等。
，当
时，n的最小值？
，试验不成功的概率都是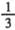
甲随机地从两套方案中选取一套进行这项试验，共试验了 3次，每次实验相互独立，且要从两套方案中等可能地选择一套.
中，
.
上任取一点
，求使
的概率；
内任作射线
，求使
B 
C 1 D 0
