题目内容
(12分)已知抛物线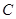 :
: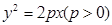 过点
过点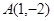 .(1)求抛物线
.(1)求抛物线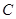 的方程,并求其准线方程;
的方程,并求其准线方程;
(2)是否存在平行于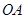 (
(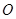 为坐标原点)的直线
为坐标原点)的直线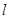 ,使得直线
,使得直线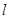 与抛物线
与抛物线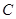 有公共点,且直线
有公共点,且直线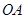 与
与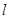 的
的
距离等于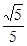 ?若存在,求出直线
?若存在,求出直线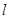 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
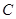 :
: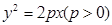 过点
过点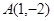 .(1)求抛物线
.(1)求抛物线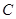 的方程,并求其准线方程;
的方程,并求其准线方程;(2)是否存在平行于
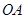 (
(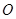 为坐标原点)的直线
为坐标原点)的直线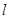 ,使得直线
,使得直线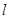 与抛物线
与抛物线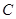 有公共点,且直线
有公共点,且直线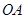 与
与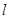 的
的距离等于
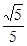 ?若存在,求出直线
?若存在,求出直线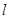 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.(1)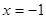 . (2)符合题意的直线存在,其方程为
. (2)符合题意的直线存在,其方程为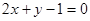 .
.
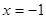 . (2)符合题意的直线存在,其方程为
. (2)符合题意的直线存在,其方程为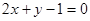 .
. 试题分析:(1)将点(1,-2)代入抛物线方程可求出p值,从而得到抛物线的方程,进而得到其准线方程.
(2) 假设存在符合题意的直线
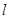 ,其方程为
,其方程为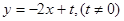 ,由于直线l与抛物线C有公共点,所以它与抛物线方程联立消去x后得到关于y的一元二次方程的判断式
,由于直线l与抛物线C有公共点,所以它与抛物线方程联立消去x后得到关于y的一元二次方程的判断式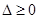 ,从而解得
,从而解得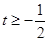 .
.然后再利用平行线间的距离公式得到t的方程求出t值,看是否满足t的范围,从而确定是否存在这样的直线.
(1)将
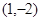 代入
代入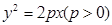 ,得
,得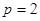 ,故所求的抛物线
,故所求的抛物线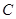 的标准方程为
的标准方程为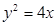 .
.其准线方程为
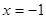 . ……… 4分
. ……… 4分(2)假设存在符合题意的直线
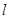 ,其方程为
,其方程为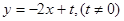 .由
.由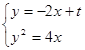 ,得
,得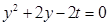 .
.因为直线
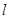 与抛物线
与抛物线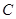 有公共点,所以
有公共点,所以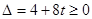 ,解得
,解得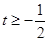 .另一方面,由直线
.另一方面,由直线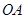 与
与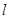 的距
的距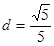 可得
可得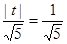 ,解得
,解得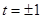 .又因为
.又因为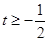 ,
,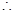
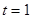 ,所以符合题意的直线存在,其方程为
,所以符合题意的直线存在,其方程为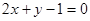 .…12分
.…12分点评:直线与抛物线的位置关系的判定可由它们的方程联立消去一个变量后得到另一个变量的二次方程,再通过判别式进行判断即可.但要注意二次项系数是否为零的问题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
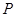 是圆
是圆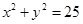 上的动点,点D是
上的动点,点D是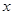 轴上的投影,M为
轴上的投影,M为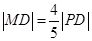
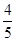 的直线被C所截线段的长度。
的直线被C所截线段的长度。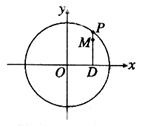
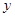 轴的负半轴上,过点
轴的负半轴上,过点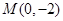 作直线
作直线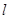 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足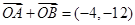 ,
,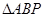 面积的的最大值.
面积的的最大值. , 则以M(4,1)为中点的弦所在直线l的方程是 .
, 则以M(4,1)为中点的弦所在直线l的方程是 . 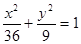 的一条弦被
的一条弦被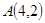 平分,那么这条弦所在的直线方程是 ( )
平分,那么这条弦所在的直线方程是 ( )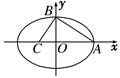
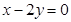
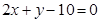
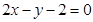
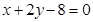
 为何值时,直线
为何值时,直线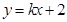 和曲线
和曲线 有两个公共点?有一个公共点?
有两个公共点?有一个公共点? 的焦点为顶点、顶点为焦点的的双曲线方程是
的焦点为顶点、顶点为焦点的的双曲线方程是



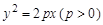 的焦点与椭圆
的焦点与椭圆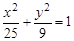 的一个焦点重合,过点
的一个焦点重合,过点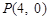 的直线与抛物线交于
的直线与抛物线交于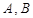 两点,若
两点,若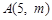 ,则
,则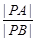 的值( )
的值( )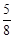
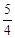
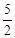
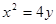 的焦点F作直线交抛物线于
的焦点F作直线交抛物线于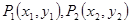 两点,若
两点,若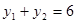 ,则
,则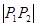 的值为( )
的值为( )