题目内容
已知平面五边形 关于直线
关于直线 对称(如图(1)),
对称(如图(1)), ,
, ,将此图形沿
,将此图形沿 折叠成直二面角,连接
折叠成直二面角,连接 、
、 得到几何体(如图(2))
得到几何体(如图(2))

(1)证明: 平面
平面 ;
;
(2)求平面 与平面
与平面 的所成角的正切值.
的所成角的正切值.
 关于直线
关于直线 对称(如图(1)),
对称(如图(1)), ,
, ,将此图形沿
,将此图形沿 折叠成直二面角,连接
折叠成直二面角,连接 、
、 得到几何体(如图(2))
得到几何体(如图(2))
(1)证明:
 平面
平面 ;
; (2)求平面
 与平面
与平面 的所成角的正切值.
的所成角的正切值.(1)证明详见解析;(2) .
.
 .
.试题分析:(1)先以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立空间直角坐标系,求出各点的坐标以及
 和
和 的坐标,进而得到两向量共线,即可证明线面平行;(2)先根据条件求出两个半平面的法向量的坐标,再求出这两个法向量所成角的余弦值,再结合同角三角函数的基本关系式可求得结果.
的坐标,进而得到两向量共线,即可证明线面平行;(2)先根据条件求出两个半平面的法向量的坐标,再求出这两个法向量所成角的余弦值,再结合同角三角函数的基本关系式可求得结果.试题解析:(1)以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立如图所示的坐标系.

由已知与平面几何知识得,


∴
 ,∴
,∴ ,∴AF∥DE,
,∴AF∥DE,又

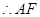 ∥
∥ 6分
6分(2)由(1)得
 四点共面,
四点共面, ,设
,设 平面
平面
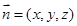 ,则
,则
不妨令
 ,故
,故 ,由已知易得平面ABCD的一个法向量为
,由已知易得平面ABCD的一个法向量为
∴
 ,设平面
,设平面 与平面
与平面 的所成角为
的所成角为

∴所求角的正切值为
 13分.
13分.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 的直线交椭圆
的直线交椭圆 ,
, 两点,
两点,  的距离为
的距离为 ,连接椭圆
,连接椭圆 .
. ,设
,设 是椭圆
是椭圆 两点的直线
两点的直线 交
交 轴于点
轴于点 ,若
,若 , 求
, 求 的取值范围;
的取值范围; 与椭圆
与椭圆 ,
, ,其中
,其中 ,若点
,若点 是线段
是线段 垂直平分线上一点,且满足
垂直平分线上一点,且满足 ,求实数
,求实数 的值.
的值. +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,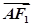 ·
· =0,3|
=0,3| |·|
|·| |=-5
|=-5 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由.
 过点
过点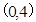 ,离心率为
,离心率为 .
. 的方程;
的方程; 且斜率为
且斜率为 的直线被椭圆所截得线段的中点坐标.
的直线被椭圆所截得线段的中点坐标. ,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知
,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知 =λ
=λ ,
, =λ
=λ ,其中0<λ<1.
,其中0<λ<1.
 +y2=1上;
+y2=1上; 是椭圆
是椭圆 的左、右顶点,椭圆
的左、右顶点,椭圆 的离心率为
的离心率为 ,右准线
,右准线 的方程为
的方程为 .
.
 是椭圆
是椭圆 交
交 ,以
,以 为直径的圆记为
为直径的圆记为 . ①若
. ①若 所得的弦长;
所得的弦长; 交于点
交于点 ,试证明:直线
,试证明:直线 与
与 轴的交点
轴的交点 为定点,并求该定点的坐标.
为定点,并求该定点的坐标. 轴上,焦距为2,直线n:x-y-1=0与椭圆C交于A、B两点,F1是左焦点,且
轴上,焦距为2,直线n:x-y-1=0与椭圆C交于A、B两点,F1是左焦点,且 ,则椭圆C的标准方程是
,则椭圆C的标准方程是  =1(a>b>0)上两点,已知m=
=1(a>b>0)上两点,已知m= ,n=
,n= ,若m·n=0且椭圆的离心率e=
,若m·n=0且椭圆的离心率e= ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点. 中,
中, 为侧面
为侧面 所在平面上的一个动点,且
所在平面上的一个动点,且 的距离是
的距离是 距离的
距离的 倍,则动点
倍,则动点