Question

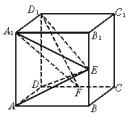
如图，正方体ABCD—A₁B₁C₁D₁中，E、F分别是BB₁、CD的中点.

（Ⅰ）证明：AD⊥D₁F；

（Ⅱ）求AE与D₁F所成的角；

（Ⅲ）证明：面AED⊥面A₁FD₁；

（Ⅳ）（理）设AA₁＝2，求三棱锥F—A₁ED₁的体积.

（文）设AA₁＝2，求三棱锥E—AA₁F的体积.

Answer 1

答案：
解析：

（Ⅰ）证明：AD⊥D1F； （Ⅱ）解：取AB中点G，连A1G、FG，因为F是CD中点，所以CFAD，又A1D1AD，所以GFA1D1，故GFD1A1是平行四边形，A1G∥D1F. 设A1G与AE交于点H，则∠AHA1是AE与D1F所成的角，因E是BB1中点，所以Rt△A1AG≌Rt△ABE，∠GA1A＝∠GAH，从而∠AHA1＝90°，即直线AE与D1F所成角为直角. （Ⅲ）证明：由（Ⅰ）知AD⊥D1F，由（Ⅱ）知AE⊥D1F，又AD∩AE＝A，所以D1F⊥面AED，又D1F面A1FD1，所以面AED⊥面A1FD1. （Ⅳ）解：（理）连GE、GD1，因为FG∥A1D，所以FG∥面A1ED1，所以体积， 因为AA1＝2， 所以面积 所以. （文）∵体积 又FG⊥面ABB1A1，三棱锥F—AA1E的高FG＝AA1＝2，