题目内容
14、f(x)=x2-4x,x∈[1,5),则这个函数值域是
[-4,5)
.分析:先对二次函数配方,结合函数在[1,5)上图象可求函数的单调性,进而可求函数的值域
解答:解:∵f(x)=x2-4x=(x-2)2-4
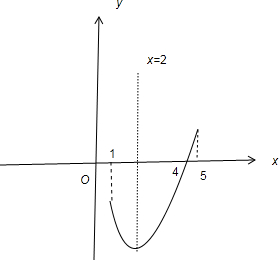
又∵x∈[1,5],而函数f(x)在[1,2]单调递减,在[2,5)单调递增
当x=2时,函数有最小值-4,当x=4时函数有最大值5
故答案为:[-4,5)
又∵x∈[1,5],而函数f(x)在[1,2]单调递减,在[2,5)单调递增
当x=2时,函数有最小值-4,当x=4时函数有最大值5
故答案为:[-4,5)

点评:本题主要考查了二次函数在闭区间上的值域(最值)的求解,解决问题的关键是要结合二次函数的图象,及函数的单调性求解,体现了数形结合的思想在解题中的应用.

练习册系列答案
相关题目