题目内容
(05福建卷) 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且 ,
,
则方程 =0在区间(0,6)内解的个数的最小值是 ( )
=0在区间(0,6)内解的个数的最小值是 ( )
| A.5 | B.4 | C.3 | D.2 |
B
解析试题分析:解:∵f(x)是定义在R上的偶函数,且周期是3,f(2)=0,∴f(-2)=0,∴f(5)=f(2)=0,f(1)=f(-2)=0,f(4)=f(1)=0,即在区间(0,6)内, f(2)=0,f(5)=0,f(1)=0,f(4)=0,故答案:B
考点:函数的奇偶性
点评:本题考查函数的奇偶性、根的存在性及个数判断.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
已知函数
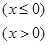 ,使函数值为5的
,使函数值为5的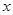 的值是( )
的值是( )
| A.-2 | B.2或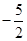 | C.2或-2 | D.2或-2或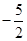 |
已知f(x)是定义在(0,+ )上的非负可导函数,且满足
)上的非负可导函数,且满足 。对任意正数a、b,若a<b,则必有( )
。对任意正数a、b,若a<b,则必有( )
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D. bf(b)≤f(a) |
函数 的单调递减区间是( )
的单调递减区间是( )
A. ,+∞) ,+∞) | B.(-∞, | C.(0, | D.[e,+∞) |
已知¦(x)是实数集R上的奇函数,且在(0,+∞)上单调递增,若¦( )=0,三角形的一个锐角A满足¦(
)=0,三角形的一个锐角A满足¦(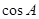 )<0,则A的取值范围是( )
)<0,则A的取值范围是( )
A.(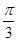 , ,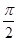 ) ) | B.(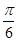 , ,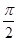 ) ) | C.(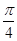 , ,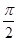 ) ) | D.(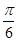 , ,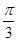 ) ) |
下列函数中,既是奇函数又是增函数的为( )
A. | B. | C. | D. |
已知a是函数 的零点,
的零点,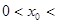 a,则
a,则 的值满足( )
的值满足( )
A. =0 =0 | B. >0 >0 | C. <0 <0 | D. 的符号不确定 的符号不确定 |
 的部分图象,其中
的部分图象,其中 ,则下列所给图象中可能正确的是 ( )
,则下列所给图象中可能正确的是 ( )

