题目内容
已知m>1,直线l:x-my-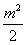 =0,椭圆C:
=0,椭圆C: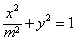 ,F1,F2分别为椭圆C的左、右焦点,
,F1,F2分别为椭圆C的左、右焦点,
(Ⅰ)当直线l过右焦点F2时,求直线l的方程;
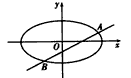
(Ⅱ)设直线l与椭圆C交于A,B两点,△AF1F2,△BF1F2的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数m的取值范围.
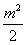 =0,椭圆C:
=0,椭圆C: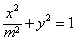 ,F1,F2分别为椭圆C的左、右焦点,
,F1,F2分别为椭圆C的左、右焦点,(Ⅰ)当直线l过右焦点F2时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A,B两点,△AF1F2,△BF1F2的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数m的取值范围.
解:(Ⅰ)因为直线l: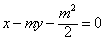 ,经过 ,经过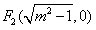 , ,所以 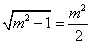 ,得m2=2, ,得m2=2,又因为m>1,所以 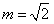 , ,故直线l的方程为  。 。(Ⅱ)设A(x1,y1),B(x2,y2), 由 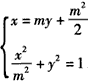 ,消去x得 ,消去x得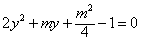 , ,则由 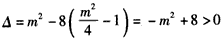 ,知 ,知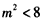 , ,且有 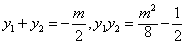 , ,由于F1(-c,0),F2(c,0),故O为F1F2的中点, 由 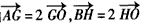 ,可知 ,可知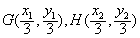 , ,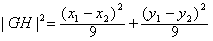 , ,设M是CH的中点,则  , ,由题意可知,2|MO|<|CH|, 即 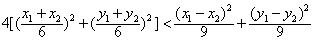 , ,即 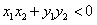 , ,而 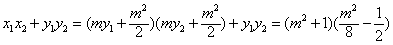 , ,所以 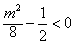 ,即m2<4, ,即m2<4,又因为m>1且Δ>0,所以1<m<2; 所以m的取值范围是(1,2). |
 |

练习册系列答案
相关题目
 已知m>1,直线
已知m>1,直线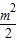 =0,椭圆C:
=0,椭圆C: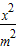 +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点.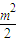 =0,椭圆C:
=0,椭圆C: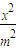 +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点.