题目内容
已知m>1,直线l:x-my-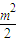 =0,椭圆C:
=0,椭圆C: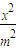 +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点.(Ⅰ)当直线l过右焦点F2时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,△AF1F2,△BF1F2的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
【答案】分析:(1)把F2代入直线方程求得m,则直线的方程可得.
(2)设A(x1,y1),B(x2,y2).直线与椭圆方程联立消去x,根据判别式大于0求得m的范围,且根据韦达定理表示出y1+y2和y1y2,根据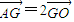 ,
,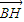 =2
=2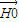 ,可知G(
,可知G(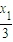 ,
,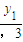 ),h(
),h(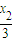 ,
,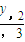 ),表示出|GH|2,设M是GH的中点,则可表示出M的坐标,进而根据2|MO|<|GH|整理可得x1x2+y1y2<0把x1x2和y1y2的表达式代入求得m的范围,最后综合可得答案.
),表示出|GH|2,设M是GH的中点,则可表示出M的坐标,进而根据2|MO|<|GH|整理可得x1x2+y1y2<0把x1x2和y1y2的表达式代入求得m的范围,最后综合可得答案.
解答: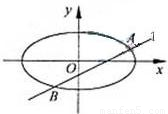 解:(Ⅰ)解:因为直线l:x-my-
解:(Ⅰ)解:因为直线l:x-my-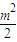 =0,经过F2(
=0,经过F2(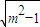 ,0),
,0),
所以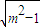 =
=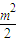 ,得m2=2,
,得m2=2,
又因为m>1,所以m=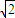 ,
,
故直线l的方程为x-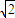 y-1=0.
y-1=0.
(Ⅱ)解:设A(x1,y1),B(x2,y2).
由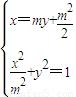 ,消去x得
,消去x得
2y2+my+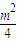 -1=0
-1=0
则由△=m2-8(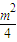 -1)=-m2+8>0,知m2<8,
-1)=-m2+8>0,知m2<8,
且有y1+y2=-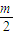 ,y1y2=
,y1y2=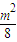 -
- .
.
由于F1(-c,0),F2(c,0),故O为F1F2的中点,
由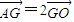 ,
,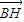 =2
=2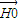 ,可知G(
,可知G(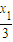 ,
,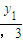 ),H(
),H(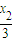 ,
, )
)
|GH|2=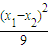 +
+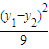
设M是GH的中点,则M(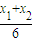 ,
,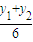 ),
),
由题意可知2|MO|<|GH|
即4[(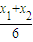 )2+(
)2+(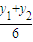 )2]<
)2]<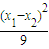 +
+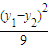 即x1x2+y1y2<0
即x1x2+y1y2<0
而x1x2+y1y2=(my1+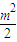 )(my2+
)(my2+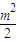 )+y1y2=(m2+1)(
)+y1y2=(m2+1)(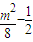 )
)
所以(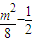 )<0,即m2<4
)<0,即m2<4
又因为m>1且△>0
所以1<m<2.
所以m的取值范围是(1,2).
点评:本题主要考查椭圆的几何性质,直线与椭圆,点与圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力.
(2)设A(x1,y1),B(x2,y2).直线与椭圆方程联立消去x,根据判别式大于0求得m的范围,且根据韦达定理表示出y1+y2和y1y2,根据
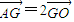 ,
,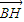 =2
=2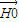 ,可知G(
,可知G(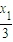 ,
,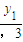 ),h(
),h(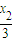 ,
,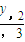 ),表示出|GH|2,设M是GH的中点,则可表示出M的坐标,进而根据2|MO|<|GH|整理可得x1x2+y1y2<0把x1x2和y1y2的表达式代入求得m的范围,最后综合可得答案.
),表示出|GH|2,设M是GH的中点,则可表示出M的坐标,进而根据2|MO|<|GH|整理可得x1x2+y1y2<0把x1x2和y1y2的表达式代入求得m的范围,最后综合可得答案.解答:
 解:(Ⅰ)解:因为直线l:x-my-
解:(Ⅰ)解:因为直线l:x-my-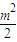 =0,经过F2(
=0,经过F2(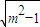 ,0),
,0),所以
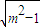 =
=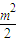 ,得m2=2,
,得m2=2,又因为m>1,所以m=
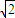 ,
,故直线l的方程为x-
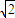 y-1=0.
y-1=0.(Ⅱ)解:设A(x1,y1),B(x2,y2).
由
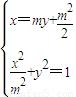 ,消去x得
,消去x得2y2+my+
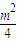 -1=0
-1=0则由△=m2-8(
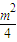 -1)=-m2+8>0,知m2<8,
-1)=-m2+8>0,知m2<8,且有y1+y2=-
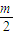 ,y1y2=
,y1y2=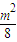 -
- .
.由于F1(-c,0),F2(c,0),故O为F1F2的中点,
由
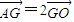 ,
,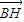 =2
=2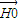 ,可知G(
,可知G(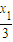 ,
,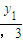 ),H(
),H(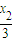 ,
, )
)|GH|2=
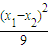 +
+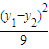
设M是GH的中点,则M(
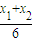 ,
,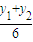 ),
),由题意可知2|MO|<|GH|
即4[(
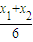 )2+(
)2+(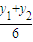 )2]<
)2]<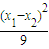 +
+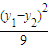 即x1x2+y1y2<0
即x1x2+y1y2<0而x1x2+y1y2=(my1+
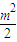 )(my2+
)(my2+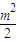 )+y1y2=(m2+1)(
)+y1y2=(m2+1)(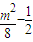 )
)所以(
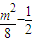 )<0,即m2<4
)<0,即m2<4又因为m>1且△>0
所以1<m<2.
所以m的取值范围是(1,2).
点评:本题主要考查椭圆的几何性质,直线与椭圆,点与圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力.

练习册系列答案
相关题目
 已知m>1,直线
已知m>1,直线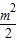 =0,椭圆C:
=0,椭圆C: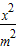 +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点.