题目内容
 已知m>1,直线l:x-my-
已知m>1,直线l:x-my-| m |
| 2 |
| x2 |
| m2 |
分析:设A(x1,y1),B(x2,y2),由直线与椭圆的方程联立消去x得到关于y的一元二次方程,由△>0可得m满足的条件,可得根与系数的关系,由
=2
,
=2
,可知G(
,
),(
,
),|GH|2=
+
?设M是GH的中点,则M(
,
),再利用2|MO|<|GH|,即可得出m的取值范围.
| AG |
| GO |
| BH |
| HO |
| x1 |
| 3 |
| y1 |
| 3 |
| x2 |
| 3 |
| y2 |
| ?3 |
| (x1-x2)2 |
| 9 |
| (y1-y2)2 |
| 9 |
| x1+x2 |
| 6 |
| y1+y2 |
| 6 |
解答:解:设A(x1,y1),B(x2,y2),由
消去x得2y2+my+
-1=0,
则由△=m2-8(
-1)=-m2+8>0,解得m2<8;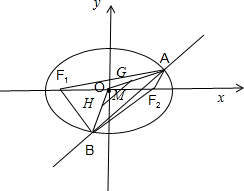
∴y1+y2=-
,y1y2=
-
.
由于F1(-c,0),F2(c,0),故O为F1F2的中点,
由
=2
,
=2
,可知G(
,
),(
,
),|GH|2=
+
?
设M是GH的中点,则M(
,
),
由题意可知2|MO|<|GH|,即4[(
)2+(
)2]<
+
,即x1x2+y1y2<0,
而x1x2+y1y2=(my1+
)(my2+
)+y1y2=(m2+1)(
-
),
∴
-
<0,即m2<4,
又因为m>1,且△>0,∴1<m<2,
∴m的取值范围是(1,2).
|
| m2 |
| 4 |
则由△=m2-8(
| m2 |
| 4 |

∴y1+y2=-
| m |
| 2 |
| m2 |
| 8 |
| 1 |
| 2 |
由于F1(-c,0),F2(c,0),故O为F1F2的中点,
由
| AG |
| GO |
| BH |
| HO |
| x1 |
| 3 |
| y1 |
| 3 |
| x2 |
| 3 |
| y2 |
| ?3 |
| (x1-x2)2 |
| 9 |
| (y1-y2)2 |
| 9 |
设M是GH的中点,则M(
| x1+x2 |
| 6 |
| y1+y2 |
| 6 |
由题意可知2|MO|<|GH|,即4[(
| x1+x2 |
| 6 |
| y1+y2 |
| 6 |
| (x1-x2)2 |
| 9 |
| (y1-y2)2 |
| 9 |
而x1x2+y1y2=(my1+
| m2 |
| 2 |
| m2 |
| 2 |
| m2 |
| 8 |
| 1 |
| 2 |
∴
| m2 |
| 8 |
| 1 |
| 2 |
又因为m>1,且△>0,∴1<m<2,
∴m的取值范围是(1,2).
点评:本题考查了椭圆的标准方程及其性质、三角形的重心定理、中点坐标公式、向量的运算、点与圆的位置关系、两点间的距离公式等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
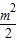 =0,椭圆C:
=0,椭圆C: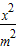 +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点.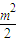 =0,椭圆C:
=0,椭圆C: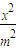 +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点.