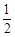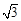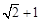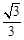题目内容
如图,在某港口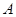 处获悉,其正东方向20海里
处获悉,其正东方向20海里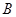 处有一艘渔船遇险等待营救,此时救援船在港口的南偏西
处有一艘渔船遇险等待营救,此时救援船在港口的南偏西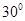 据港口10海里的
据港口10海里的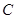 处,救援船接到救援命令立即从
处,救援船接到救援命令立即从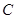 处沿直线前往
处沿直线前往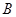 处营救渔船.
处营救渔船.
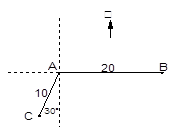
(Ⅰ) 求接到救援命令时救援船据渔船的距离;
(Ⅱ)试问救援船在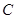 处应朝北偏东多少度的方向沿直线前往
处应朝北偏东多少度的方向沿直线前往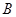 处救援?(已知
处救援?(已知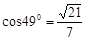 ).
).
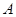 处获悉,其正东方向20海里
处获悉,其正东方向20海里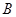 处有一艘渔船遇险等待营救,此时救援船在港口的南偏西
处有一艘渔船遇险等待营救,此时救援船在港口的南偏西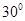 据港口10海里的
据港口10海里的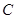 处,救援船接到救援命令立即从
处,救援船接到救援命令立即从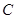 处沿直线前往
处沿直线前往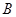 处营救渔船.
处营救渔船.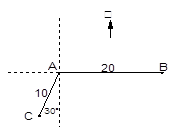
(Ⅰ) 求接到救援命令时救援船据渔船的距离;
(Ⅱ)试问救援船在
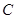 处应朝北偏东多少度的方向沿直线前往
处应朝北偏东多少度的方向沿直线前往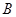 处救援?(已知
处救援?(已知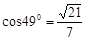 ).
). (Ⅰ) 接到救援命令时救援船据渔船的距离为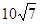 海里.
海里.
(Ⅱ)救援船应沿北偏东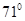 的方向救援.
的方向救援.
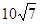 海里.
海里.(Ⅱ)救援船应沿北偏东
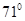 的方向救援.
的方向救援.本题考查正弦定理、余弦定理在三角形中的应用,注意方位角与计算的准确性,考查计算能力.
(Ⅰ):△ABC中,求出边长AB,AC,∠CAB,利用余弦定理求出BC,即可求接到救援命令时救援船据渔船的距离;
(Ⅱ)△ABC中,通过正弦定理求出sin∠ACB的值,结合已知数据,得到∠ACB即可知道救援船在C处应朝北偏东多少度的方向沿直线前往B处救援.
解:(Ⅰ) 由题意得: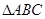 中,
中,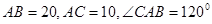 ,
,
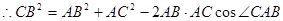 ……………3分
……………3分
即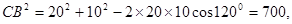
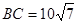 ,所以接到救援
,所以接到救援
命令时救援船据渔船的距离为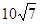 海里. ……………6
海里. ……………6
(Ⅱ)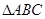 中,
中, 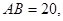
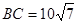 ,
,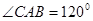 ,由正弦定理得
,由正弦定理得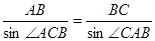 即
即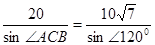
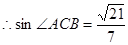 ………9分
………9分
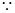
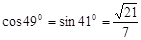 ,
,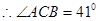 ,
,
故救援船应沿北偏东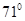 的方向救援. …………… 12分
的方向救援. …………… 12分
(Ⅰ):△ABC中,求出边长AB,AC,∠CAB,利用余弦定理求出BC,即可求接到救援命令时救援船据渔船的距离;
(Ⅱ)△ABC中,通过正弦定理求出sin∠ACB的值,结合已知数据,得到∠ACB即可知道救援船在C处应朝北偏东多少度的方向沿直线前往B处救援.
解:(Ⅰ) 由题意得:
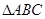 中,
中,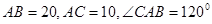 ,
,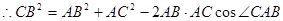 ……………3分
……………3分即
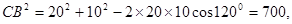
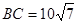 ,所以接到救援
,所以接到救援命令时救援船据渔船的距离为
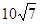 海里. ……………6
海里. ……………6(Ⅱ)
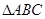 中,
中, 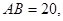
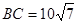 ,
,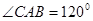 ,由正弦定理得
,由正弦定理得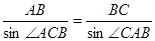 即
即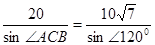
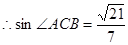 ………9分
………9分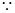
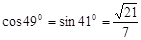 ,
,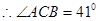 ,
,故救援船应沿北偏东
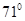 的方向救援. …………… 12分
的方向救援. …………… 12分
练习册系列答案
相关题目
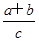 的取值范围是
的取值范围是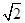 ) C.(1,
) C.(1,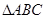 中,角
中,角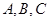 所对的边分别是
所对的边分别是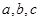 ,且满足
,且满足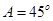 ,
,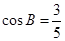 .
.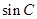 的值;
的值;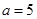 ,求
,求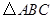 的面积.
的面积.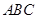 中,角A、B、C所对的边分别是 a,b,c且a="2,"
中,角A、B、C所对的边分别是 a,b,c且a="2," 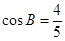
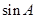 的值.
的值.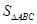 =3,求b,c的值.
=3,求b,c的值.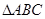 中,角
中,角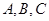 所对的边为
所对的边为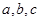 ,已知
,已知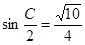 。
。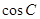 的值;
的值;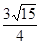 ,且
,且 ,求
,求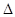 ABC中,
ABC中,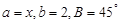 ,若该三角形有两个解,则x的取值范围是_______.
,若该三角形有两个解,则x的取值范围是_______.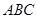 中,
中,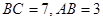 ,且
,且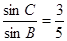 .
.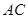 ; (Ⅱ)求
; (Ⅱ)求 .
.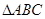 中,若
中,若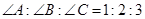 ,则
,则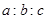 等于( )
等于( )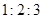
 满足:
满足: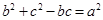 ;
; 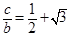 , 则
, 则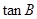 的值是
的值是