题目内容
【题目】已知椭圆
，点
， 
是椭圆
上的动点.
（Ⅰ）若直线
与椭圆
相切，求点
的坐标；
（Ⅱ）若
在
轴的右侧，以
为底边的等腰
的顶点
在
轴上，求四边形
面积的最小值.
【答案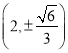】(Ⅰ) 
；(Ⅱ) 
.
【解析】试题分析：
(Ⅰ)联立直线与椭圆的方程，利用判别式等于零可得
，据此可得点
的坐标为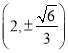
.
(Ⅱ)利用几何关系可得
是以
为底边的等腰三角形，结合题意可得面积函数：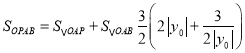 
，当且仅当
等号成立.则四边形
面积的最小值为
.
试题解析：
（Ⅰ）设直线
的方程为
，
联立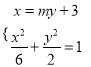
消去
可得： 
，
故
，解得
，
从而
，解得
， 
.所以，点
的坐标为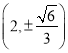
.
（Ⅱ）设线段
的中点为
.因
是以
为底边的等腰三角形，故
.
由题意，设
，则点
的坐标为
，
且直线
的斜率
，故直线
的斜率为
，
从而直线
的方程为： 
.又
令
，得
，化简得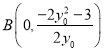
.
所以，四边形
的面积
.
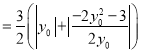
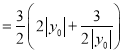
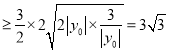等号成立.
所以，四边形
面积的最小值为
.
【题目】某汽车美容公司为吸引顾客，推出优惠活动：对首次消费的顾客，按
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠，标准如下：
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
该公司从注册的会员中, 随机抽取了
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为
元, 根据所给数据, 解答下列问题:
（1）估计该公司一位会员至少消费两次的概率；
（2）某会员仅消费两次, 求这两次消费中, 公司获得的平均利润；
（3）以事件发生的频率作为相应事件发生的概率, 设该公司为一位会员服务的平均利润为
元, 求
的分布列和数学期望
．
【题目】《太阳的后裔》是第一部中国与韩国同步播出的韩剧，爱奇艺视频网站在某大学随机调查了110名学生，得到如表列联表：由表中数据算得K2的观测值k≈7.8，因此得到的正确结论是（ ）
女 | 男 | 总计 | |
喜欢 | 40 | 20 | 60 |
不喜欢 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
（K2≥k） | 0.100 | 0.010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
附表：K2= 
．
A.有99%以上的把握认为“喜欢该电视剧与性别无关”
B.有99%以上的把握认为“喜欢该电视剧与性别有关”
C.在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”
D.在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
【题目】已知某中学高三文科班学生共有
人参加了数学与地理的水平测试，现学校决定利用随机数表法从中抽取
人进行成绩抽样统计，先将
人按
进行编号．
（Ⅰ）如果从第
行第
列的数开始向右读，请你依次写出最先检测的
个人的编号；（下面摘取了第
行 至第
行）
（Ⅱ）抽的
人的数学与地理的水平测试成绩如下表：
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地 理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 |
| 4 |
| |
成绩分为优秀、良好、及格三个等级，横向、纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有
人，若在该样本中，数学成绩优秀率为
，求
的值．
（Ⅲ）将
的
表示成有序数对
，求“在地理成绩为及格的学生中，数学成绩为优秀的人数比及格的人数少”的数对
的概率．
