题目内容
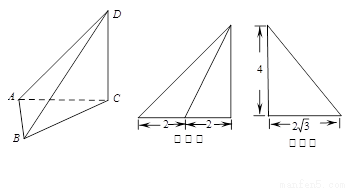
(理)如图9所示,等腰△ABC的底边AB=66,高CD=3.点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P—ACFE的体积.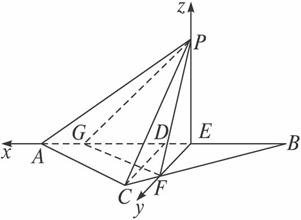
图9
(1)求V(x)的表达式.
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值.
答案:(理)分析:本小题主要考查函数、函数极值、导数及其应用、几何体体积、空间异面直线所成的角等基础知识,考查数形结合的数学思想方法,以及空间想象能力、推理论证能力、运算求解能力、创新意识.
解:(1)∵EF⊥AB,∴EF⊥PE.又∵PE⊥AE,EF∩AE=E,且PE在平面ACFE外,∴PE⊥平面ACFE.∵EF⊥AB,CD⊥AB,∴EF∥CD.∴![]()
![]() EF=
EF=![]() .
.
∴四边形ACFE的面积S四边形ACFE=S△ABC-S△BEF=![]() ×
×![]() ×3-
×3-![]() ×
×![]() x2=
x2=![]() x2.
x2.
∴四棱锥P—ACFE的体积VP—ACFE=![]() S四边形ACFE·PE=
S四边形ACFE·PE=![]() x3,即V(x)=
x3,即V(x)=![]() x3(0<x<
x3(0<x<![]() ).
).
(2)由(1)知V′(x)=![]() x2.令V′(x)=0
x2.令V′(x)=0![]() x=6.∵当0<x<6时,V′(x)>0,当6<x<
x=6.∵当0<x<6时,V′(x)>0,当6<x<![]() 时,V′(x)<0,∴当BE=x=6时,V(x)有最大值,最大值为V(6)=
时,V′(x)<0,∴当BE=x=6时,V(x)有最大值,最大值为V(6)=![]() .
.
(3)解法一:如图,以点E为坐标原点,向量![]() 、
、![]() 、
、![]() 分别为x、y、z轴的正向建立空间直角坐标系,
分别为x、y、z轴的正向建立空间直角坐标系,

则E(0,0,0),P(0,0,6),F(0,![]() ,0),A(6
,0),A(6![]() -6,0,0),C(3
-6,0,0),C(3![]() -6,3,0).
-6,3,0).
于是![]() =(-3
=(-3![]() ,3,0),
,3,0),![]() =(0,
=(0,![]() ,-6).AC与PF所成角θ的余弦值为
,-6).AC与PF所成角θ的余弦值为
cosθ=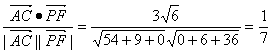 .
.
∴异面直线AC与PF所成角的余弦值为![]() .
.
解法二:过点F作FG∥AC交AE于点G,连结PG,则∠PFG为异面直线AC与PF所成的角.
∵△ABC是等腰三角形,
∴△GBF也是等腰三角形.
于是FG=BF=PF=![]() ,从而PG=
,从而PG=![]() .
.
在△GPF中,根据余弦定理得cos∠PFG=![]() =
=![]() .
.
故异面直线AC与PF所成角的余弦值为![]() .
.

练习册系列答案
相关题目



 及其三视图中的主视图和左视图如图9所示,则棱
及其三视图中的主视图和左视图如图9所示,则棱 的长为_________.
的长为_________.