题目内容
(理)如图a所示,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,AC=BC=a,AA1=AB,E是AB1上的点.(1)求二面角B1-AC-B的平面角的正切值;
(2)如何确定点E的位置,使得GE⊥AB1?并求此时C、E两点的距离.
(文)如图b所示,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,AC=BC=a,AA1=AB,C点在AB1上的射影为E,D为AB的中点.
(1)求证:AB1⊥平面CED;
(2)求二面角B1-AC-B的平面角的正切值.

第17题图
答案:(理)(1)∵AC⊥平面B1BCC1
∴AC⊥B1C,又AC⊥BC
∴∠B1CB是二面角B1-AC-B的平面角
在Rt△B1BC中,B1B=AB=![]() ,BC=a
,BC=a
∴tan∠B1CB=![]() .
.
即二面角B1-AC-B的平面角的正切值为![]() .
.
(2)作CD⊥AB,垂足为D,作DE⊥AB1,垂足为E,
∵CD⊥AB,CD⊥AB1’∴CD⊥平面A1ABB1
∴CD⊥AB1,又DE⊥AB1
∴AB1⊥平面EDC,∴AB1⊥EC
即此时E点即为所求.
Rt△EDC中,DC=![]() a,ED=
a,ED=![]() AD=
AD=![]()
∴EC=![]() .
.
(文)(1)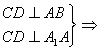 CD⊥平面A1ABB1
CD⊥平面A1ABB1
∴ AB1⊥平面CED
AB1⊥平面CED
(2)∵AC⊥BC,ACE⊥C1C,AC⊥平面B1BCC1
∴AC⊥B1C,又AC⊥BC
∴∠B1CB是二面角B1-AC-B的平面角
在Rt△B1BC中,B1B=AB=![]() a,BC=a
a,BC=a
∴tan∠B1CB=![]() .
.
即二面角B1-AC-B的平面角的正切值为![]() .
.

练习册系列答案
相关题目
 如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点. 如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
