题目内容
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= AD=a,G是EF的中点,
AD=a,G是EF的中点,(1)求证:AG⊥平面BGC;
(2)求二面角B-AC-G的正弦值.
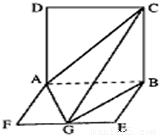
【答案】分析:(1)先证明AG⊥BG,又由平面ABCD⊥平面ABEF,ABCD是正方形,结合面面垂直的性质,我们易得到BC⊥平面ABEF,进而由线面垂直的定义得到BC⊥AG,由线面垂直的判定定理,即可得到结论;
(2)作GM⊥AB于M,则M为AB中点,M为G的射影,作GH⊥AC于H,连接MH,从而可知所求角∠GHM,进而可求.
解答: (1)证明:∵G是矩形ABEF的边EF的中点
(1)证明:∵G是矩形ABEF的边EF的中点
∴AG=BG=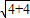 =2
=2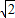
∴AG2+BG2=AB2
∴AG⊥BG
又∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
且BC⊥AB
∴BC⊥平面ABEF,
又∵AG?平面ABEF,
∴BC⊥AG
∵BC∩BG=B
∴AG⊥平面BGC;
(2)解:作GM⊥AB于M,则M为AB中点,M为G的射影
作GH⊥AC于H,连接MH,则所求角∠GHM
∵GM=a,MH=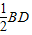 =
= a
a
∴GH=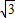 a
a
∴sin∠GHM=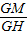 =
=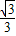 .
.
点评:本题以面面垂直为载体,考查面面垂直的判定与性质,考查面面角,关键是正确运用定理,寻找线面垂直.
(2)作GM⊥AB于M,则M为AB中点,M为G的射影,作GH⊥AC于H,连接MH,从而可知所求角∠GHM,进而可求.
解答:
 (1)证明:∵G是矩形ABEF的边EF的中点
(1)证明:∵G是矩形ABEF的边EF的中点∴AG=BG=
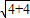 =2
=2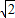
∴AG2+BG2=AB2
∴AG⊥BG
又∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
且BC⊥AB
∴BC⊥平面ABEF,
又∵AG?平面ABEF,
∴BC⊥AG
∵BC∩BG=B
∴AG⊥平面BGC;
(2)解:作GM⊥AB于M,则M为AB中点,M为G的射影
作GH⊥AC于H,连接MH,则所求角∠GHM
∵GM=a,MH=
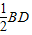 =
= a
a∴GH=
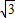 a
a∴sin∠GHM=
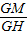 =
=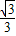 .
.点评:本题以面面垂直为载体,考查面面垂直的判定与性质,考查面面角,关键是正确运用定理,寻找线面垂直.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
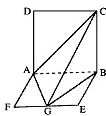 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.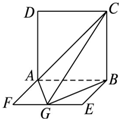 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=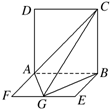 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=