题目内容
运货卡车以每小时x千米的速度匀速行驶1300千米(50≤x≤100)(单位:千米/小时).假设柴油的价格是每升6元,而汽车每小时耗油(6+
)升,司机的工资是每小时24元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
| x2 | 360 |
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
分析:(1)根据题意可得,行车所用的时间为t=
小时,根据行车总费用=耗费柴油的费用+司机的工资,即可列出行车总费用y关于x的表达式;
(2)根据(1)中的函数关系式,运用基本不等式,即可求得答案,注意等号成立的条件.
| 1300 |
| x |
(2)根据(1)中的函数关系式,运用基本不等式,即可求得答案,注意等号成立的条件.
解答:解:(1)设行车所用的时间为t,则t=
小时,次行车总费用为y,
根据行车总费用=耗费柴油的费用+司机的工资,可得
y=
×6×(6+
)+24×
,50≤x≤100,
化简整理可得,y=
+
,50≤x≤100,
故这次行车总费用y关于x的表达式为:y=
+
,50≤x≤100;
(2)由(1)可知,y=
+
,50≤x≤100,
∴y=
+
≥2
=2600,
当且仅当
=
,即x=60时取“=”,
∴当x=60时,y取得最大值为2600,
故当x=60时,这次行车的总费用最低为2600元.
| 1300 |
| x |
根据行车总费用=耗费柴油的费用+司机的工资,可得
y=
| 1300 |
| x |
| x2 |
| 360 |
| 1300 |
| x |
化简整理可得,y=
| 78000 |
| x |
| 65 |
| 3x |
故这次行车总费用y关于x的表达式为:y=
| 78000 |
| x |
| 65 |
| 3x |
(2)由(1)可知,y=
| 78000 |
| x |
| 65 |
| 3x |
∴y=
| 78000 |
| x |
| 65 |
| 3x |
|
当且仅当
| 78000 |
| x |
| 65 |
| 3x |
∴当x=60时,y取得最大值为2600,
故当x=60时,这次行车的总费用最低为2600元.
点评:本题主要考查函数模型的选择与应用,基本不等式在最值问题中的应用.在应用基本不等式求最值时要注意“一正、二定、三相等”的判断.运用基本不等式解题的关键是寻找和为定值或者是积为定值,难点在于如何合理正确的构造出定值.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
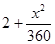 )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.