题目内容
运货卡车以每小时x千米的速度匀速行驶130千米(60≤x≤100).假设汽油的价格是每升2元,而汽车每小时耗油(2+| x2 | 360 |
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
分析:(1)由题意先设行车所用时间t,利用速度、路程、时间的关系列出t与x的关系式,再求得这次行车总费用y关于x的表达式即可;
(2)欲求x为何值时,这次行车的总费用最低,利用导数知识研究(1)中函数的单调性从而求得其最小值即可.
(2)欲求x为何值时,这次行车的总费用最低,利用导数知识研究(1)中函数的单调性从而求得其最小值即可.
解答:解:(1)设行车所用时间为t=
(h),y=
×2×(2+
)+
,x∈[60,100]
所以,这次行车总费用y关于x的表达式是y=
+
x(x∈[60,100])
(2)y,=-
+
>0
所以y=
+
x(x∈[60,100])为增函数.
所以,当x=60时,这次行车的总费用最低,最低费用为
元
| 130 |
| x |
| 130 |
| x |
| x2 |
| 360 |
| 14×130 |
| x |
所以,这次行车总费用y关于x的表达式是y=
| 2340 |
| x |
| 13 |
| 18 |
(2)y,=-
| 2340 |
| x2 |
| 13 |
| 18 |
所以y=
| 2340 |
| x |
| 13 |
| 18 |
所以,当x=60时,这次行车的总费用最低,最低费用为
| 247 |
| 3 |
点评:本小题主要考查函数模型的选择与应用、导数的应用及函数的最值,函数的最值要由极值和端点的函数值确定.当函数定义域是开区间且在区间上只有一个极值时,这个极值就是它的最值.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
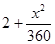 )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.